Il faut se rendre à l’évidence : la géométrie est une abstraction totale.
Elle parle d’objets qui n’existent pas : le point est non-mesurable et indivisible, la ligne n’a pas d’épaisseur, le cercle est inapte à la quadrature et à la mesure.
Cela commence par penser UN. Là ça crépite, et j’entends Unité. Voilà, c’est dit et cela devient le problème d’une référence commune, qui est la base d’un accord sur cette mesure à partir de laquelle on peut l’augmenter, la multiplier. Que ce soit le mètre, le gramme, la coudée, un segment, l’individu… tout le problème est là. Il ne peut y avoir de solidarité qu’entre individus partageant un système symbolique qui rend possible un consensus sur le sens du monde.

Pour géométriser, commençons par représenter le « Un » par un trait qui sert de mesure de référence.
Quelle solitude ! Donc, on va le répliquer, soit semblable à lui-même, soit en l’augmentant d’une unité. Leur relation géométrique fait apparaître quelque chose que l’on appelle un nombre irrationnel parce que sa valeur numérique ne peut être définie, elle est une tension vers l’infiniment (le nombre de décimales ne s’arrêtent pas). Cela me laisse penser que dans toute relation, il y a de l’inconnu insurmontable en tant que tel.
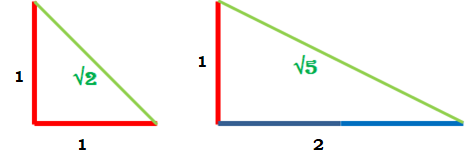
Vous me direz quel rapport avec le nombre d’or, j’y viens mais avant j’explique.
Les nombres peuvent avoir des relations particulières (comme les humains).
Les relations entre eux se révèlent, entre autres, dans les formes. La proportion entre les formes voilà ce qui va constituer la nature de la relation.
Ainsi, il existe des sous-ensembles de tous les nombres possibles si on veut qu’ils vérifient un rapport de proportion, on appelle cela un rapport d’analogie.
– Seul un sous-ensemble de tous les nombres possibles, vérifient un rapport d’analogie tel a/b = c/d = e/f (Exemple : 6/2 = 12/4 = 48/16…. Ici le rapport vaut 3. Avec d’autres nombres il pourrait valoir une multitude de valeur. Exemple : 20/4 = 60/12 = 250/50 …ici le rapport vaut 5.
– Si on ramène à trois le nombre d’éléments mis en relation, seul un sous-ensemble plus restreint de tous les nombres possibles vérifient un rapport d’analogie tel a/b = c/a (Exemple : 21/7 = 63/21, ici le rapport vaut également 3 ; avec d’autres trois nombres, il pourrait valoir une multitude de valeur. Exemple : 20/4 = 100/20, ici le rapport vaut 5.
– Il existe un ensemble encore plus restreint de nombres qui, lorsque l’on ramène à deux le nombre d’éléments mis en rapport, vérifient le rapport d’analogie tel que a/b = (a+b)/a.
La valeur de ce rapport est unique[1] et vaut (1+√5)/2.
Les mesures a et b sont alors dans une proportion d’harmonie dite aussi divine ou dorée, appelée le nombre d’or. On le désigne par la lettre grecque Φ (phi).
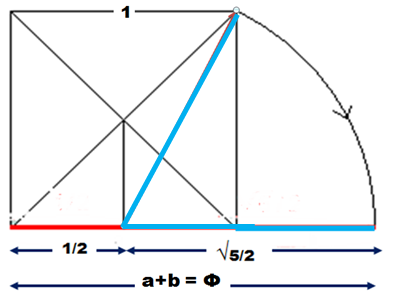
La valeur (1+√5)/2 du nombre d’or montre qu’elle est un partage, en 2, des valeurs de l’Unité (b) à laquelle on ajoute sa relation (√5) avec son double (a).
Les mesures sont fonction de la valeur de l’unité. Ce qui reste c’est la proportion par report avec le compas (ou le cordeau) des éléments de la composition.
Ces mesures exactes ne peuvent pas être calculées puisqu’elles font intervenir des nombres irrationnels, mais elles peuvent être montrées.
On appelle irrationnels les nombres qui ont une expansion décimale infinie, sans motif répétitif. Cela signifie que si l’on écrit un irrationnel sous forme décimale, les chiffres continuent indéfiniment sans jamais former de séquence régulière.
Qu’est-ce que cela veut dire en dehors de la géométrie qui n’est qu’un support symbolique de réflexions ?
Dans toutes relations, les mots de l’harmonie humaine tels que «fraternité», «amour», «solidarité», «démocratie», «liberté»… ne peuvent se mesurer que quand on les montre dans l’action qui est leur forme incarnée, sinon ils restent incomplets de cette humanité justement contenue dans cet infini des décimales des nombres irrationnels.
Mais on peut penser ce rapport d’harmonie en termes de relations humaines.
Si a domine ou contrôle b, alors il faut qu’il y ait une «convention», une «règle» ou une «loi», régissant leur rapport, qui puisse dominer ou contrôler a. Il est entendu que a et b peuvent être des individus ou des groupes sociaux !
Au plan architectural, cela voudrait dire que l’exploration de certains nombres, fondement et régulation de tracés architecturaux, nous conduirait à la compréhension du principe même de l’harmonie. Ainsi, par un jeu indéfini de résonances de rythmes qui se reflètent et se répondent, la construction s’élève, devient aérienne, en même temps qu’elle élève l’homme qui la contemple (ou y participe) et le fait communiquer avec le beau, le vrai, le bien qui ne sont que les diverses appellations de l’harmonie universelle.

Spirituellement, dans la relation entre le Un et le Deux (√5) , entre le non manifesté et la dualité de la création, il y a un impossible à atteindre qui échappe à la raison, un inatteignable qui se montre dans l’infini des décimales de Phi encore à trouver, merveilleusement imagé par Michel Ange par la séparation des mains sur la Création d’Adam au plafond de la chapelle Sixtine.
Comment approcher le nombre d’or ?
Le rôle mystique et organisateur du Nombre dans l’art éternel des Anciens est souvent concrétisé par le Nombre d’Or qui garde un grand prestige et sonne à nos oreilles plein de séduction (Michel Baglis, Le Nombre d’or, p.100)
Le nombre d’or n’est pas une quantité mais l’expression d’une relation dans un rapport particulier, un entre-deux harmonieux.
Au IIIe siècle avant J-C., Euclide évoque le partage d’un segment en « extrême et moyenne raison » dans le livre VI des Éléments : Une droite est dite coupée en extrême et moyenne raison quand, comme elle est toute entière (a+b) relativement au plus grand segment (a), ainsi est le plus grand relativement au plus petit (b) ; autrement dit a/b = (a+b)/a. C’est Platon qui en aurait fait ensuite un sujet d’étude spécifique.

Cette proportion d’harmonie, dite aussi dorée, est une proportion analogique, a/b = (a+b)/a, elle vaut (1 + √5) / 2. (Rappelons que √5 est la valeur de la diagonale du rectangle de dimension 1 sur 2 appelé double carré).

Lire le texte Alberti et l’harmonie spatiale, miroir de l’harmonie cosmique

En 1509, Fra Luca Pacioli, un moine professeur de mathématiques, le nomme «La divine proportion» dans son ouvrage illustré par son ami Léonard de Vinci. Ce sont des considérations de théologie chrétienne qui justifient aux yeux du moine Pacioli, dans son ouvrage La Divine proportion, l’importance accordée à la dite proportion dont les caractéristiques concordent avec les attributs qui appartiennent à Dieu.
Au chapitre 5 du Tome premier (sur 33) de son livre La divine proportion, Luca Pacioli donne les raisons qui l’ont incité à appeler «divine proportion» le nombre d’or :
– Il est unique, et l’unité est «l’épithète» suprême de Dieu lui-même,
– Le nombre d’or se définit à partir de trois longueurs comme la Sainte Trinité constituée du Père, du Fils et du Saint Esprit.
– Le fait que le nombre d’or soit irrationnel répond à l’impénétrabilité des voies du Seigneur…
Pacioli assimile l’omniprésence et l’immutabilité divines à l’autosimilarité dont témoigne le nombre d’or qui ne dépend pas de la longueur du segment divisé …
Pacioli affuble donc les effets de la divine proportion d’un adjectif : essentiel, singulier, merveilleux, suprême, incompréhensible etc.
De même que Dieu ne peut se définir en termes propres et que les paroles ne peuvent nous le faire comprendre, ainsi notre proportion ne se peut jamais déterminer par un nombre que l’on puisse connaître, ni exprimer par quelque quantité rationnelle, mais est toujours mystérieuse et secrète, et qualifiée par les mathématiciens d’irrationnelle.
Ce sont des considérations de théologie chrétienne qui justifient aux yeux du moine Pacioli, dans son ouvrage la divine proportion, l’importance accordée à la dite proportion dont les caractéristiques concordent avec les attributs qui appartiennent à Dieu… Le premier est l’unicité… Le deuxième attribut concordant est celui de la Sainte Trinité ; c’est-à-dire que, de même qu’en Dieu une seule substance réside en trois personnes, le Père, le Fils et l’Esprit Saint, de la même façon, il convient qu’un même rapport ou proportion se trouve toujours entre trois termes. Troisième attribut : De même que Dieu ne peut se définir en termes propres et que les paroles ne peuvent nous le faire comprendre, ainsi notre proportion ne se peut jamais déterminer par un nombre que l’on puisse connaître, ni exprimer par quelque quantité rationnelle, mais est toujours mystérieuse et secrète, et qualifiée par les mathématiciens d’irrationnelle. Quatrième attribut : De même que Dieu ne peut jamais changer et est tout en tout et tout entier dans chaque partie, de même notre présente proportion est toujours la même et toujours invariable… Cinquième attribut : De même que Dieu confère l’être à la Vertu Céleste appelée Quinte Essence, et par elle aux quatre autres corps simples, c’est à dire aux quatre éléments Terre, Eau, Air et Feu… de même notre sainte proportion donne l’être formel au ciel même, selon Platon qui dans son Timée attribue au ciel la figure du corps appelé dodécaèdre… lequel ne se peut former sans notre proportion… et Pacioli de montrer les propriétés des cinq corps platoniciens circonscrits dans la sphère et le rôle éminent de la divine proportion dans la construction de deux d’entre eux : l’icosaèdre et du dodécaèdre.
Une remarque : ne manquez pas de parcourir L’ouvrage de Fra Pacioli. Outre les solides dessinés par Léonard de Vinci, découvrez les lettrines de Fra Pacioli construites sur des rapports de formes géométriques (à partir de la p. 139/318)

C’est Théodore Andréa Cook (1867-1928) qui décida avec son ami mathématicien américain Mark Barr de proposer la notation φ (la lettre grecque Phi) comme symbole mathématique du nombre d’or en référence à Phidias, le sculpteur grec Phidias (490-430 avant notre ère) qui décora le Parthénon à Athènes. Ce nombre fut ensuite appelé Der goldene Schnitt, c’est-à-dire la section dorée, par le philosophe allemand Adolf Zeising.
On le trouve ainsi avec les noms suivants : Nombre scandaleux car irrationnel (Platon) ; Proportion d’extrême et moyenne raison (Euclide) ; Proportion d’Euclide (Fibonacci) ; Section dorée (sectio aurea, Vinci) ; Phi (φ-expression mathématique, Théodore Cook) ; Proportion dorée (selon l’usage courant).
Au début du XXe siècle, le diplomate roumain Matila Ghyka lui donne, en 1932, le nom de nombre d’or. Il s’appuie sur les travaux de Zeising et du physicien allemand Gustav Théodor Fechner ; ses ouvrages, L’esthétique des proportions dans la nature et dans les arts (1927) et Le Nombre d’or. Rites et rythmes pythagoriciens dans le développement de la civilisation occidentale (1931), insistent sur la prééminence du nombre d’or et établissent définitivement le mythe de ce nombre.
Parmi tous les ouvrages, le mémoire Nombre d’or et proportions dans les ouvrages en pierres de Simon Darves-Blanc est intéressant parce qu’écrit par un compagnon opératif contemporain.
Encore un peu de lecture avec Le nombre d’or à la portée de tous par D. Neroman
Au Moyen Âge, les savants, les pères de l’église, les bâtisseurs, les maîtres d’ouvrages ou maîtres d’œuvre, se réclament de la doctrine platonicienne des corps cosmiques, les cinq polyèdres réguliers et font du nombre d’or un modèle de perfection esthétique et philosophique.
Les bâtisseurs de cathédrales utilisaient ainsi 5 unités relatives au corps humain – la quine – reliées par la proportion divine. La ligne (longueur d’un grain d’orge), l’unité de base, est égale 2,247 mm. (Le nombre d’or et la main esthétique dune_proportion ou réalité anatomique)
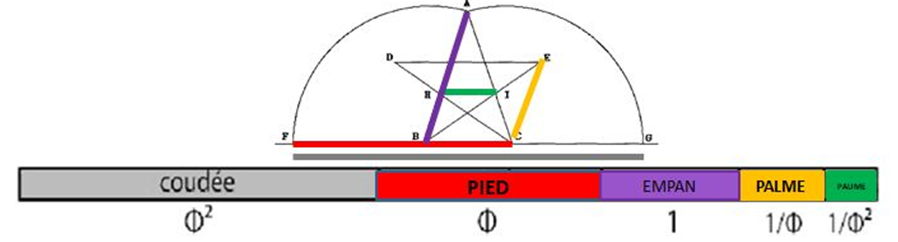
En alchimie, ce nombre est le nombre d’aur, de la lumière. Toute figure construite selon ses proportions, comme l’étoile à cinq branches, est une fenêtre qui ouvre sur la pure lumière, celle qui n’est pas faite de particule, représentant, outre les 4 éléments, celui qui les domine, la quintessence qui pourrait s’appeler le nom-ombre d’or.
Nous devrions dire les nombres d’or.
Pythagore et sa femme Théano les déclinèrent dans tous les sens possibles, sous toutes les formes de rectangle, de pentacle, d’étoile ou de pentagone, les traquant et mettant ainsi en valeur les théorèmes antérieurs de Thalès.
Partout où on peut mettre en évidence sur un tracé une mesure de √5 ou de 1+√5, il faut traquer le nombre d’or et trouver les deux éléments qu’il met rapport harmonieux, sa valeur approchée doit rester présente à l’esprit du compagnon : 1,618…
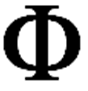
Ou mieux encore, La forme de la lettre grecque Phi nous dit que le cercle et la ligne suffisent pour exprimer l’harmonie du monde.
Il est à remarquer que si l’on prend 1,618… pour valeur de Phi et 3,14… , pour valeur de Pi, on peut dire que (Phi x Pi)2 tend vers 26, la valeur, en guématrie du tétragramme יהוה (YHVH).
Le carré long
Il trouve une de ses définitions en Franc-Maçonnerie dans le catéchisme de l’apprenti : – Quelle est la figure de la loge ? – un carré long. – Quelle est sa longueur ? – de l’orient à l’occident. – Quelle est sa largeur ? – du nord au midi. Ce carré long reste un carré, aussi long que large et couvrant la totalité de la surface de la Terre. Et si l’on se réfère, une fois de plus, au catéchisme de ce degré, le carré long a une profondeur et une hauteur : il part du nadir, centre de la Terre, et s’élève en altitude au zénith, sur des coudées sans nombre. Le carré long est donc un objet de dimensions infinies qui embrasse symboliquement l’univers dans son ensemble. Carré en extension, c’est-à-dire en devenir, le carré long devient une géométrie initiatique, une cosmogonie illuminatrice.
Lors de la consécration d’une Loge maçonnique au Rite égyptien, le tracé de l’espace sacré réservé au pavé mosaïque se fait à l’aide d’une corde à 12 nœuds séparés d’une coudée. On forme ainsi un triangle mesurant 3, 4, et 5 nœuds. Une fois déterminée l’orientation du Temple, on applique ce triangle sur le sol, puis on en trace les contours à la craie. Après l’avoir déplacé dans l’autre sens, on l’applique à nouveau sur le sol de manière à fermer le rectangle et on en trace également les contours. Ainsi, sans règle ni compas, est formé un carré long déterminant le centre même de l’espace sacré du Temple, là où s’entrecroisent les deux hypoténuses (diagonales).
Si le carré long de dimension 1 sur 2 (le double carré), image du lieu de culte, formalise la communion des hommes avec le Divin, le rectangle d’or, carré long de proportion dorée, illustre une autre notion, celle de la fraternité des hommes entre eux.
Le double carré est à la base des tracés fondés sur le nombre d’or, sa diagonale ayant pour valeur √5.
Le rectangle d’or est aussi appelé carré long ; mais il a la particularité que le grand côté et le petit côté sont partagés selon extrême et moyenne raison, autrement dit, la dimension de sa longueur divisée par celle de sa largeur est égale au nombre d’or.
À partir du double carré et de sa diagonale se construit le carré long, appelé rectangle d’or qui est de nature lunaire. Le carré lunaire est un carré de gestation de passage qui permet de tracer, entre autres, la spirale ; c’est un carré matrice.

Une bonne approximation d’un rectangle d’or peut être construite à l’aide de carrés dont les côtés sont égaux aux nombres de la suite de Fibonacci. Le pavé mosaïque de dimension 5 sur 8 s’approche, ainsi, des calibres d’un rectangle d’or.
Si on prend un rectangle d’or et qu’on lui retire un carré construit sur son petit côté, on obtient un autre rectangle d’or plus petit mais de même proportion, duquel on pourra encore détacher un carré pour obtenir un autre rectangle d’or et ainsi de suite à l’infini. De même, si on ajoute à un rectangle d’or un carré on obtient un nouveau rectangle, plus grand mais respectant à son tour les mêmes proportions. Par analogie, les frères et sœurs, passés à l’Orient éternel, sont les carrés qui se détachent ; les nouveaux compagnons, avec la taille de leur pierre cubique (carré), s’incorporent à un rectangle doré pour former un nouveau rectangle doré plus grand.
La connaissance du nombre d’or est si importante qu’elle se trouve rendue visible par la pierre cubique à pointe et/ou par le tablier de l’apprenti, pointe relevée, qui viennent s’ajuster sous le pentagramme.
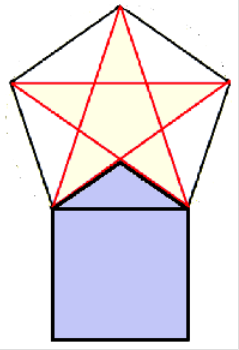
Et maintenant, pour quelques mouvements du compas et de la règle, quelques tracés à faire et refaire ou refaire.
Pour trouver la dimension de Phi sur un segment
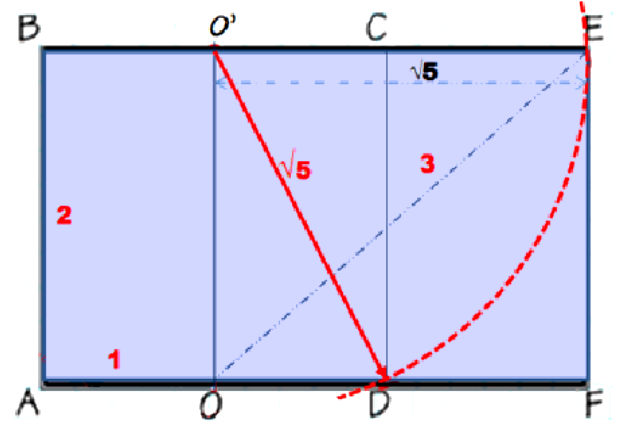
Le Tracé du rectangle d’or
- Tracer un carré ABCD
- Tracer la médiatrice du segment AD qui donne les points O et O’
- Reporter, au compas O’D sur le prolongement de BC, noter E leur point d’intersection
- Tracer la perpendiculaire à BE
- Prolonger AD qui coupe la perpendiculaire de BE en F
AB = 2 unités, AO = 1 unité ; la diagonale OE = 3 unités. Le rectangle ABEF obtenu est un rectangle d’or ; la longueur et la largeur sont dans un rapport du nombre d’or
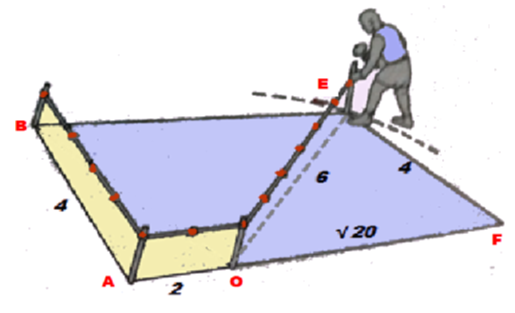
Le principe de ce processus utilisant le théorème de Pythagore, tracé avec règle et compas par le maître d’œuvre, est ensuite reporté au sol grâce à la corde à 13 (112 espaces)nœuds. Par exemple, en utilisant 4 espaces pour AB, 2 pour AO et donc 6 pour OE, on obtient un rectangle d’or ABEF .
Et cela sans avoir à passer par les mathématiques qui démontrent que les dimensions (2 + √20)/4 – soit (2+4,7213)/4 – donnent un rapport, entre largeur et longueur, d’environ 1,61803, valeur considérée comme le nombre d’or. ABEF est pratiquement un rectangle d’or.
Du rectangle d’or au théorème de Pythagore
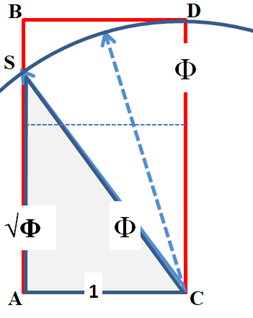
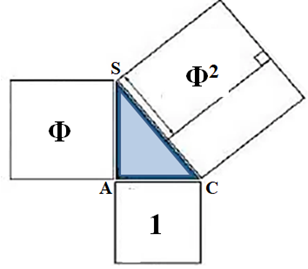
Le triangle de Képler associe le théorème de Pythagore et le nombre d’or par la figure construite à partir du rectangle d’or (parfois appelé le visage de Dieu), où les dimensions respectives des côtés des carrés sont Φ, 1 et √Φ.
Dans un rectangle d’or ABCD, à partir de C, prendre comme rayon la longueur CD (Φ) et reporter le sur le côté AB qui donne le point S, sommet du triangle rectangle de Képler (SAC). Le côté AS2 = Φ2-1 = Φ soit AS = √Φ
Le Tracé de la spirale dans le rectangle d’or
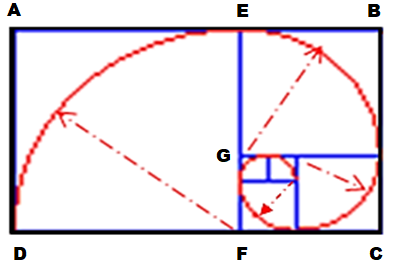
- Tracer un rectangle d’or ABCD. Pour faciliter le tracé on peut se contenter d’un rectangle d’or approximatif construit sur la suite de Fibonacci en partant d’un carré de 1×1.
- Prendre A comme centre de cercle de rayon r = AD. Tracer l’arc de cercle qui coupe AB en E.
- Prendre D comme centre de cercle de même rayon r = AD. Tracer l’arc de cercle qui coupe DC en F.
- Tracer le carré AEFD
- Recommencer ce processus dans le rectangle d’or EBCF pour tracer le carré EBHG
- Continuer dans le rectangle d’or GHCF et ainsi de suite jusqu’à…
- Pour obtenir la spirale, tracer le quart de cercle de centre F et de rayon FD, le quart de cercle de centre G et de rayon EG,
Une autre spirale peut être tracée, à main levée, par des arcs joignant les points de croisement des diagonales de chacun des carrées
Le nombre Phi en couleurs
Choisissons arbitrairement 10 couleurs attachées aux 10 chiffres.
(Attention nous les conserverons pour faire la même chose avec le nombre PI, dans le prochain article). Par exemple.

Prenons les 99 décimales telles qu’elles sont calculées et je vous propose une image sous forme d’un carré 10/10 de cette valeur approchée de Phi (qui restera toujours approchée). 1,618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137…

Pour vous en faire comprendre l’incommensurable du nombre d’or en voici une autre Valeur approchée
1.618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137484754088075386891752126633862223536931793180060766726354433389086595939582905638322661319928290267880675208766892501711696207032221043216269548626296313614438149758701220340805887954454749246185695364864449241044320771344947049565846788509874339442212544877066478091588460749988712400765217057517978834166256249407589069704000281210427621771117778053153171410117046665991466979873176135600670874807101317952368942752194843530567830022878569978297783478458782289110976250030269615617002504643382437764861028383126833037242926752631165339247316711121158818638513316203840052221657912866752946549068113171599343235973494985090409476213222981017261070596116456299098162905552085247903524060201727997471753427775927786256194320827505131218156285512224809394712341451702237358057727861600868838295230459264787801788992199027077690389532196819861514378031499741106926088674296226757560523172777520353613936210767389376455606060592165894667595519004005559089502295309423124823552122124154440064703405657347976639723949499465845788730396230903750339938562102423690251386804145779956981224457471780341731264532204163972321340444494873023154176768937521030687378803441700939544096279558986787232095124268935573097045095956844017555198819218020640529055189349475926007348522821010881946445442223188913192946896220023014437702699230078030852611807545192887705021096842493627135925187607778846658361502389134933331223105339232136243192637289106705033992822652635562090297986424727597725655086154875435748264718141451270006023890162077732244994353088999095016803281121943204819643876758633147985719113978153978074761507722117508269458639320456520989698555678141069683728840587461033781054443909436835835813811311689938555769754841491445341509129540700501947754861630754226417293946803673198058618339183285991303960720144559504497792120761247856459161608370594987860069701894098864007644361709334172709191433650137157660114803814306262380514321173481510055901345610118007905063814215270930858809287570345050780814545881990633612982798141174533927312080928972792221329806429468782427487401745055406778757083237310975915117762978443…
[1] Posons a/b = F ;
a/b = (a+b)/a donne a/b = a/a + b/a soit F = 1 + 1/F,
en multipliant tout par F, on obtient F2 = F + 1 ou encore F2 – F – 1 = 0.
On a une équation du second degré qui donne deux solutions (racines de l’équation). L’une d’elles étant négative, on ne retient que l’autre d’où F = (√5 +1)/2. Le calcul donne une valeur approchée du nombre d’or de 1,618…………..

