Nous invitons les lecteurs qui abordent pour la première fois un article sur le symbolisme pythagoricien à se reporter aux articles traitant du delta (Voir aussi l’article de Marie Delclos) ou à celui traitant de l’étoile à cinq branches qui comportent une courte introduction expliquant l’importance du pythagorisme en Franc-maçonnerie.
Un point commun
Les deux pierres, dans les instructions par questions et réponses « servent aux compagnons à aiguiser leurs outils », bien que ni l’une ni l’autre ne semble être appropriée à cet usage ! C’est là une énigme proposée au compagnon… Pour comprendre son grade, il est censé la résoudre.
Nous y reviendrons…
La pierre cubique
Comme son nom l’indique, la pierre cubique a la forme d’un cube. Le rituel du Rite Écossais Rectifié précise même qu’il s’agit d’une « pierre cubique à six faces » ! C’est un pléonasme volontaire, qui permet aux rédacteurs du rituel d’insister sur le lien entre le cube, le nombre 6 et les nombres en général.
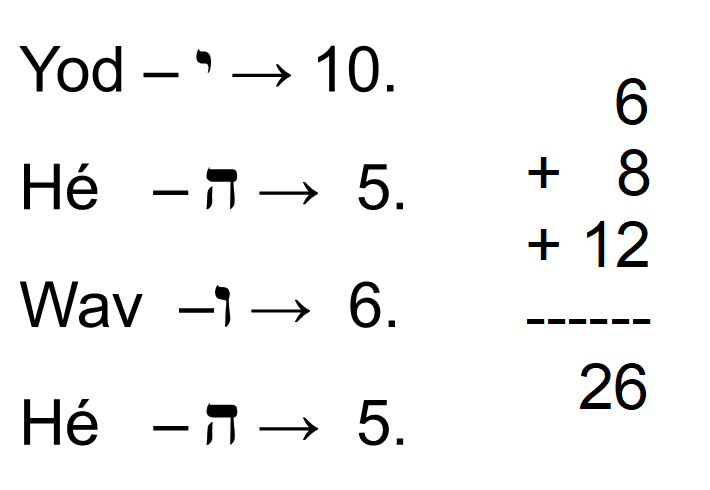
Il faudra donc se souvenir du fait que le cube a six faces, huit sommets, douze arêtes.
On a coutume d’additionner ces trois nombres ce qui donne vingt-six, le nombre correspondant au nom divin de quatre lettres.
Pour les pythagoriciens, comme pour les kabbalistes ce nombre est très important parce que 26 – 1 = 25 est le carré de cinq et 26 + 1 = 27 est le cube de 3… Si on retranche 1 à 26 on obtient un carré et si on lui ajoute 1 on obtient un cube. Le grand mathématicien Fermat a conjecturé que vingt-six est le seul nombre entier à jouir de cette propriété. Nous ne savons pas si cette conjecture a été démontrée, mais elle semble, démontrée ou non, être une évidence car les courbes des deux fonctions x2 et x3 sont divergentes et cette divergence croît avec la valeur de x.
Par ailleurs, 26 est le double de 13 qui est le septième nombre premier et le cinquième nombre second obtenu à partir de 2.
Définitions pythagoriciennes :
Un nombre premier est divisible seulement par 1 et par lui-même.
Un nombre second est le produit de deux nombres premiers : 2 x 3 est le premier nombre second.
Relevons aussi que :
Six est le premier nombre parfait (1 x 2 x 3 = 6 et 1+ 2 + 3 = 6)
Huit est le premier cube.
Douze est le premier nombre sublime (il a 6 diviseurs 1, 2, 3, 4, 6, 12 – 6 est un nombre parfait et la somme de ses diviseurs est 28 qui est également un nombre parfait).
Nous ne savons pas si les pythagoriciens ont connu les nombres sublimes, il n’en est, à notre connaissance, pas question dans leurs œuvres et de nos jours on n’en connaît que deux, le second, écrit en base 10 comporte 76 chiffres. Les ordinateurs actuels ne son pas assez puissants pour calculer le troisième !
Cela dit, les pythagoriciens tenaient 12 en haute estime parce qu’il est la somme de 3, 4 et 5.
La progression 6, 8, 12, les nombres premiers et les pyramides.
Si on retranche 1 à chaque nombre de cette progression on obtient la suite de trois nombres premiers consécutifs : 5, 7, 11. Il en résulte que les nombres 6,8,12 sont les pyramidaux de rang 2 d’ordre 5, 7, 11. Soit de trois nombres premiers consécutifs.
Passons maintenant à l’aspect géométrique
Le cube et le concept de « centre du monde »
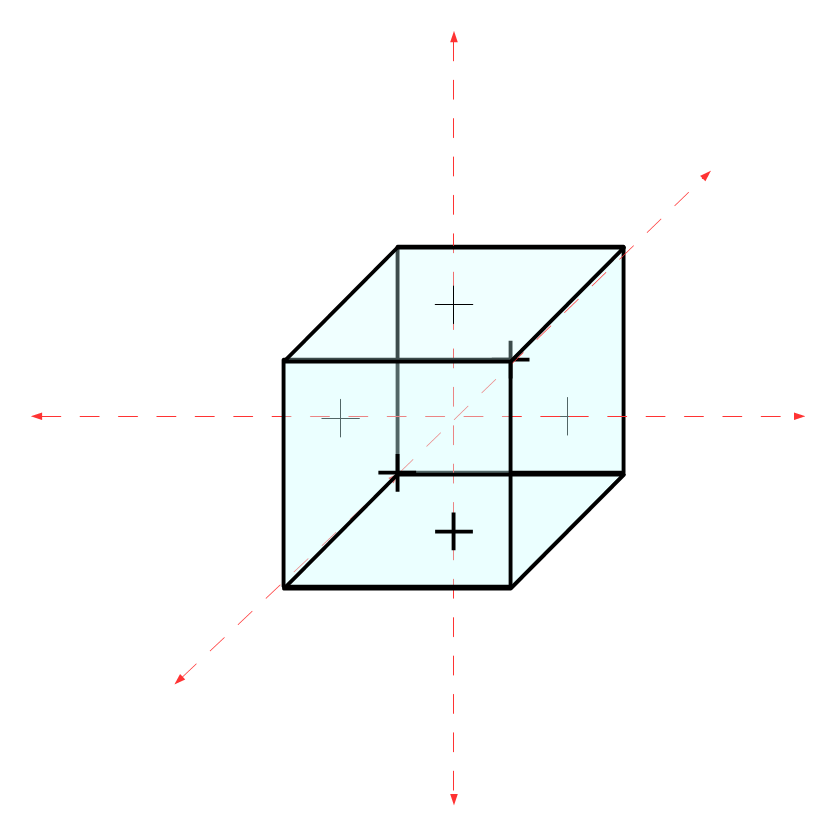
Parce qu’il a six faces, le cube est un symbole du centre, et plus particulièrement du « centre du monde créé ».
Ainsi la Mecque, qui d’après les musulmans est le centre du monde a un temple cubique, autour duquel les pèlerins doivent accomplir des circumbulations.
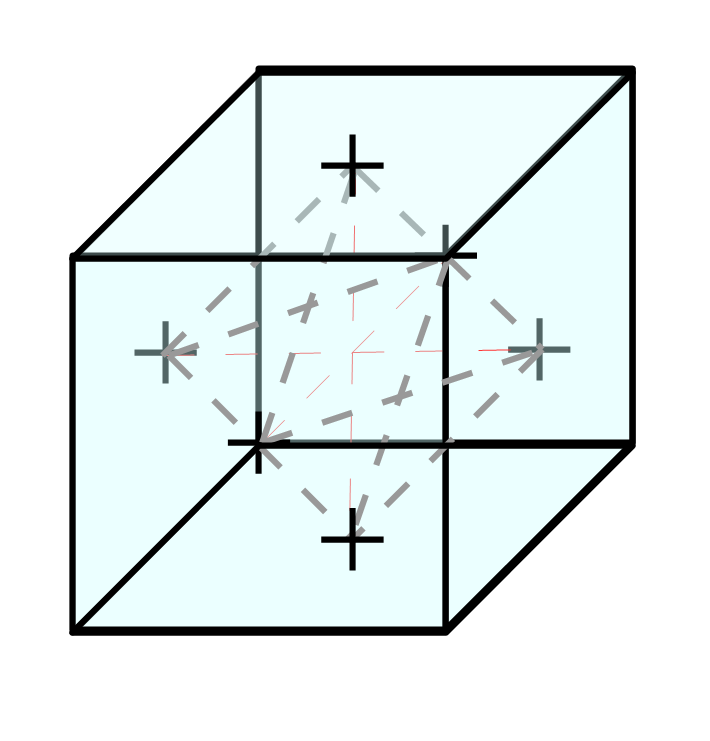
Par ailleurs, le cube, a pour solide réciproque l’octaèdre qui a six sommets, huit faces et douze arêtes. Comme les arêtes de cet octaèdre joignent entre eux les centres des faces du cube on sait que les diagonales de l’octaèdre sont égales au côté du cube.
Si on donne à ce côté la valeur 1 l’arête de l’octaèdre réciproque est racine de deux sur deux. C’est une inversion du théorème de de Pythagore :
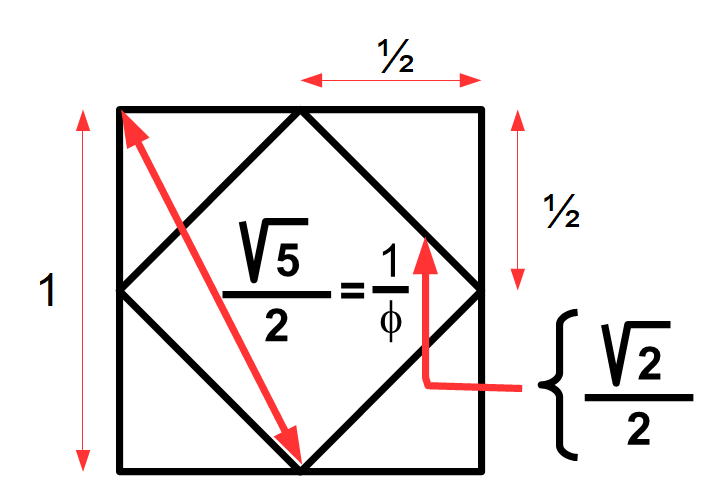
La diagonale d’un octaèdre forme avec deux arêtes un triangle rectangle dont elle est l’hypoténuse, donc la somme du carré des deux arêtes est égale à 1, le carré d’une arête est donc égal à ½ et la racine carrée de ½ est égale à racine de deux sur deux (le carré de racine de deux est deux, celui de deux est 4 et 2/4 est égal à ½). Comme le montre la vue en coupe ci-contre le cube a aussi un rapport avec phi, le nombre d’or (voir l’article sur l’étoile flamboyante). Evidemment puisque ces considérations sont vraies pour la coupe du cube, elles s’appliquent au carré.
Le cube et les nombres diagonaux
Ces considérations nous amènent évidemment à considérer le rapport du cube avec les nombres diagonaux.
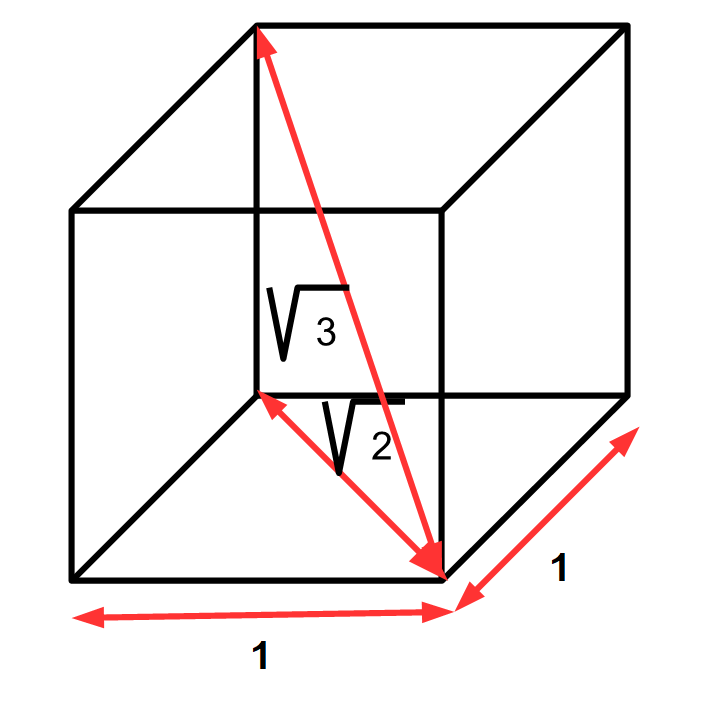
Si on considère la diagonale du cube sa mesure est racine de trois, ce qui met le cube en rapport avec le triangle isocèle (ou régulier) inscrit dans le cercle de rayon 1(voir l’article a propos du delta lumineux).
Ces nombres nous serviront pour la construction de la pierre ou plutôt des pierres cubiques à pointe car l’iconographie nous en montre avec des pyramidions de hauteurs différentes.
Le cube et la sphère
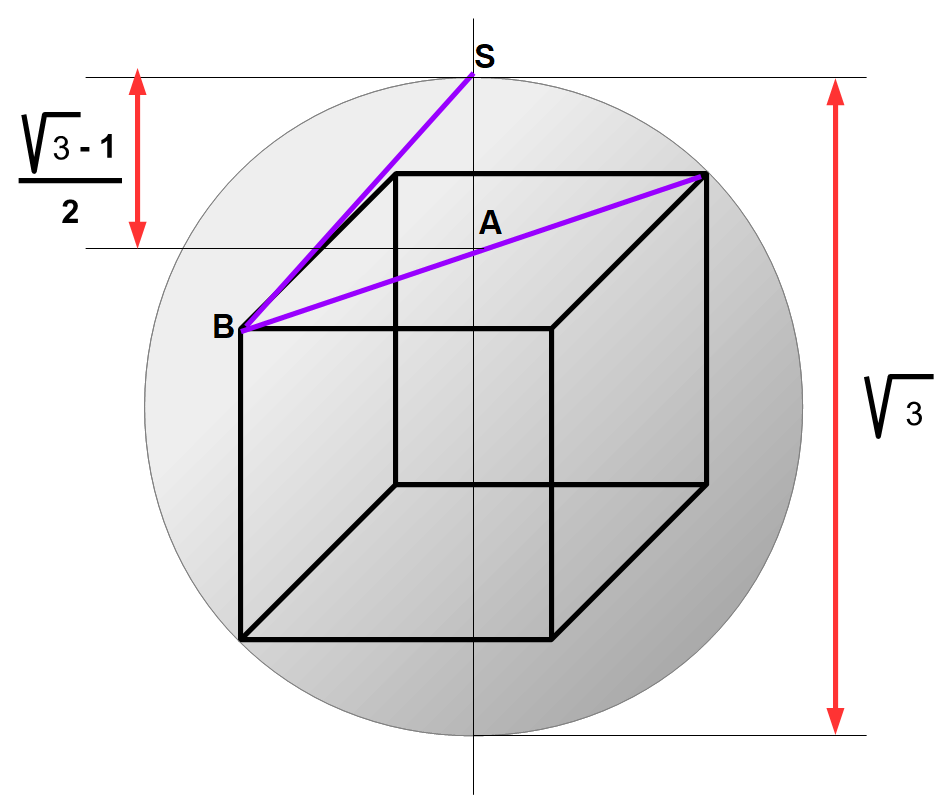
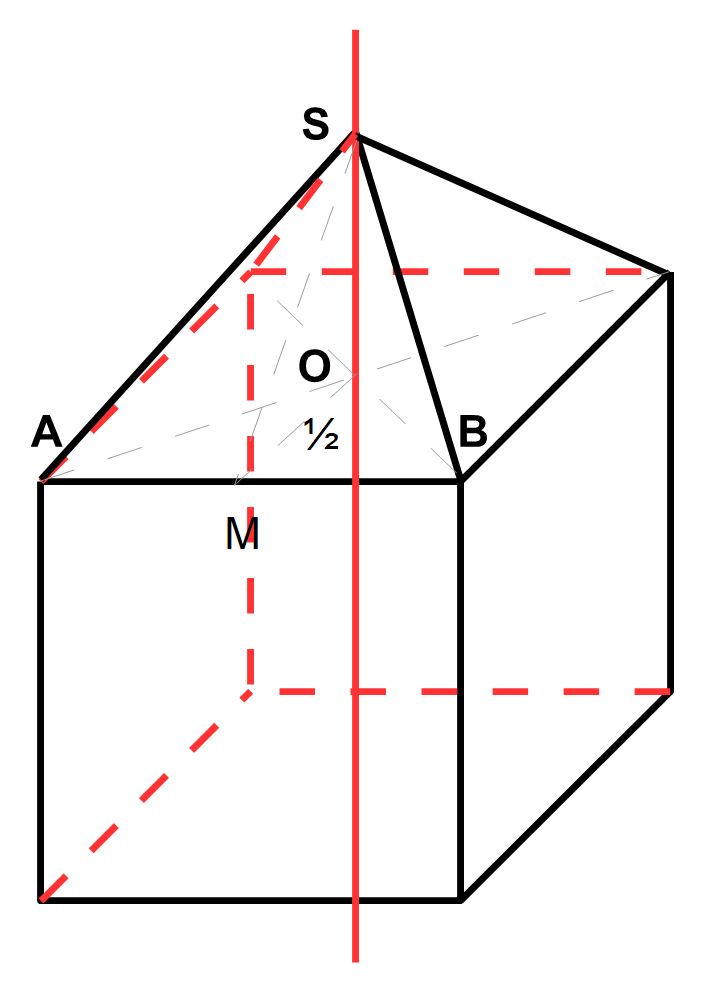
La sphère exinscrite au cube a pour diamètre la mesure de la diagonale de ce cube puisque les huits sommet du cube doivent toucher la surface de la sphère. Il en résulte que la hauteur (S A) du triangle rectangle (S A B) est égale à racine de 3 moins un divisé par deux.
Quant à la sphère inscrite dans le cube, son diamètre est égal à celui du côté du cube (dans notre cas 1).
Le cube développé.
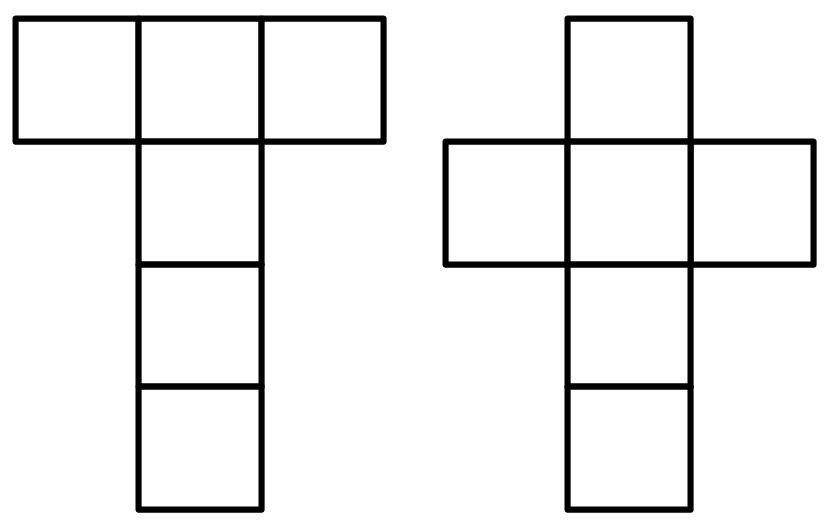
Le cube développé forme soit une croix latine, ce qui nous renvoie à nouveau à l’axe et au centre du monde, soit la lettre grecque Tau. Cette lettre fut utilisée dans les premiers temps du christianisme en place de la croix (x) qui est le Tav de l’alphabet hébreu archaïque… Quant au sens symbolique de la croix, il est bien antérieur au christianisme et quand le jour du mercredi des cendres le prêtre marque le front de chaque fidèle d’une croix, il appose certes le « signe du Christ » en même temps que celui du Père mais en outre il affirme que chaque fidèle est le « centre du monde ». L’affirmation est certes symbolique ; tout comme chacun de nos temples s’étend du septentrion au midi, de l’Orient à l’Occident et du Zénith au Nadir (à moins que sa hauteur ne soit « des coudées sans nombre » et que sa profondeur aille « jusqu’au centre de la Terre ») Dans un cas comme dans l’autre ces affirmations placent notre temple au centre du monde tout comme elles y placent celui qui pour une raison quelconque serait étendu mort ou vif sur le pavé mosaïque qui en marque le centre… On remarquera que les directions Orient-Occident, Septentrion – Midi, Zénith – Nadir qui se croisent au centre de chacun de nous, au centre de notre temple, au centre de la Terre… au centre de chaque grain de poussière forment une magnifique croix six branches. Croix que l’on peut observer au sommet de toutes les églises d’Orient et qui est souvent suggérée à la pointe des clochetons des églises gothiques.
Les pierres cubiques à pointe remarquables
Si on s’en tient aux textes des rituels, la pierre cubique à pointe est unique. C’est une pierre cubique surmontée d’un pyramidion, ou d’une pyramide si l’on préfère puisqu’un pyramidion est par définition une : « Petite pyramide quadrangulaire qui termine un obélisque » et qu’une pierre cubique paraît un peu courte pour être confondue avec un obélisque. Elle est unique, mais l’iconographie nous en présente de multiples images. N’en doutons pas, dans le passé, ceux qui ont taillé ou moulé (certaines son en plâtre et d’autres en matière plastique) les pierres cubiques à pointe de nos temples n’ont pas donné au pyramidion n’importe quelle pente. Bien au contraire ils ont choisi avec soin les dimensions de cette pyramide pour « renforcer le sens du symbole ». Bien que leurs efforts aient été louables, ils n’ont rien renforcé ! Quel que soit son angle au sommet, la pointe de la pierre cubique symbolise toutes les pointes possibles.
Cela dit, nous ne sommes pas allés dans tous les temples de la planète mesurer l’angle au sommet des pierres cubiques à pointe. Par ailleurs les angles qui présentent un intérêt ne sont pas nombreux.
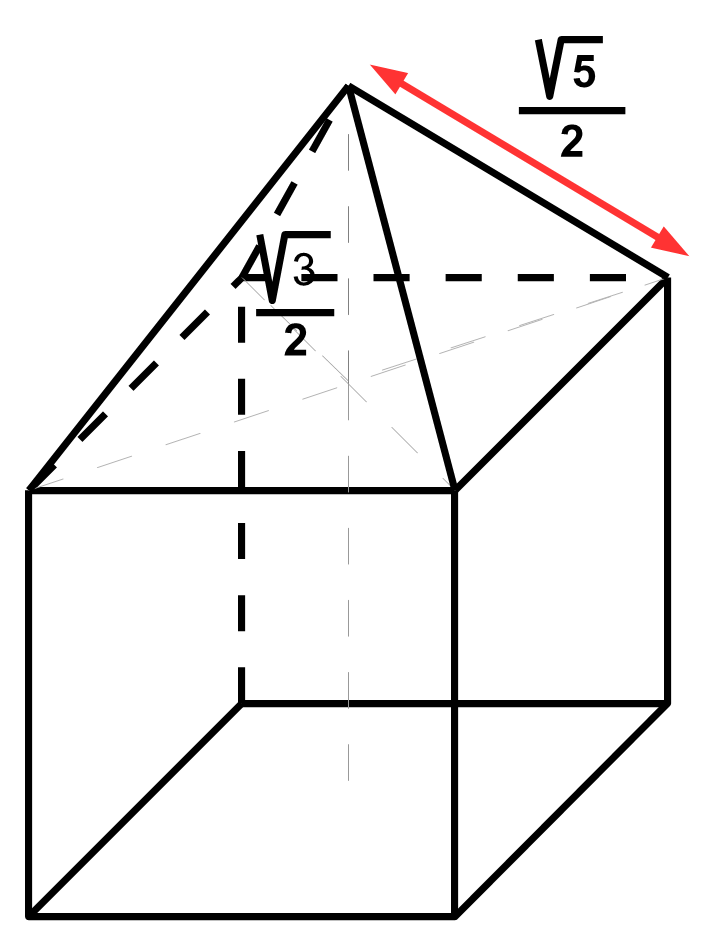
La pointe du pyramidion touche la sphère circonscrite au cube
Le premier d’entre eux, et le plus évident est évidemment celui qui amène la pointe du pyramidion à toucher le pôle de la sphère circonscrite.
Remarquons que cette « pente » n’a rien de remarquable à part le fait qu’elle est commune à tous les cubes inscrits dans une sphère… A moins, bien entendu que quelque chose nous ait échappé !
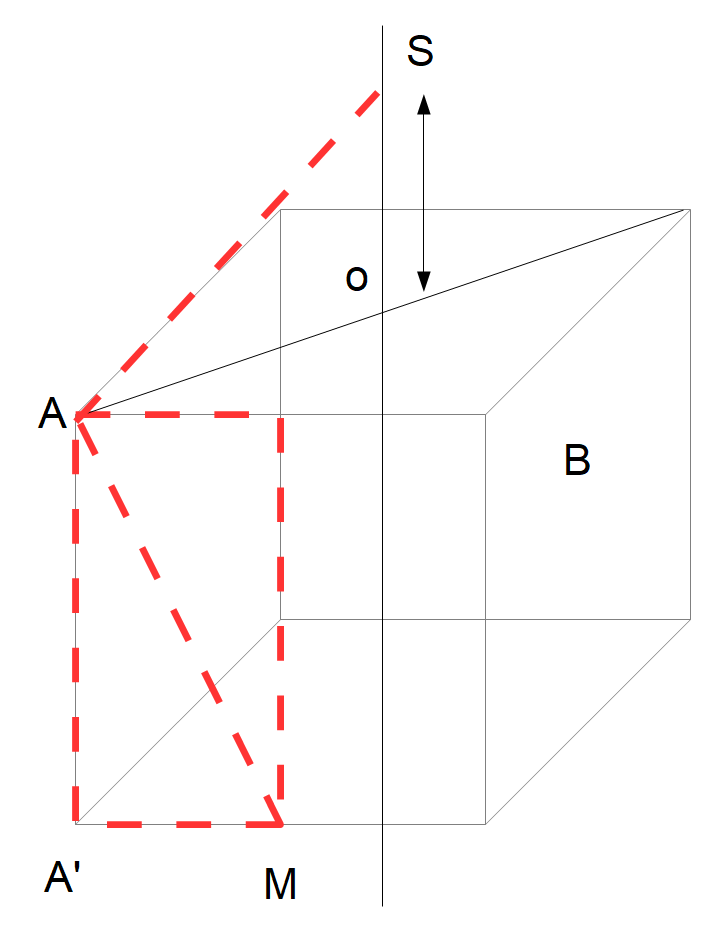
La distance de pointe du pyramidion a un angle du cube est la moitié de racine de cinq.
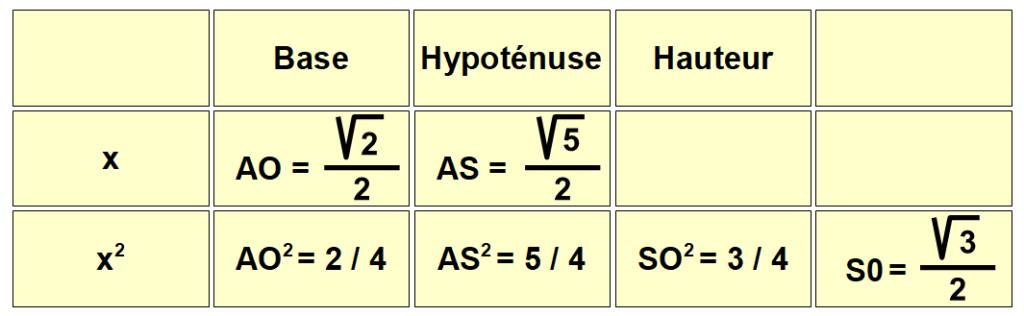
Si l’arête du pyramidion est égale à l’inverse Racine de cinq sur deux sa hauteur est égale à la moitié de la diagonale du cube !
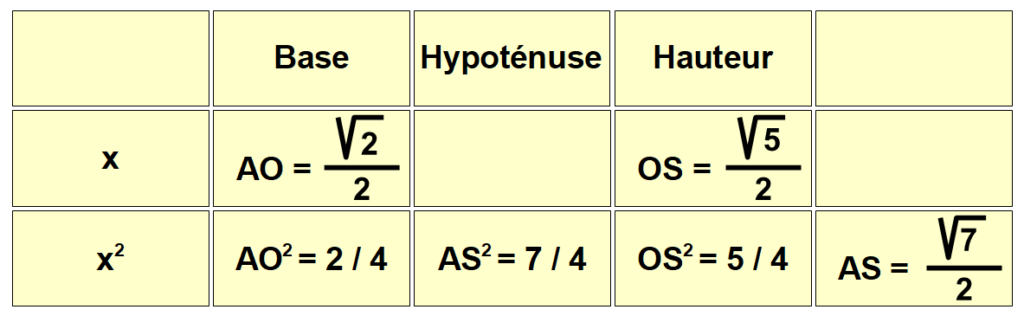
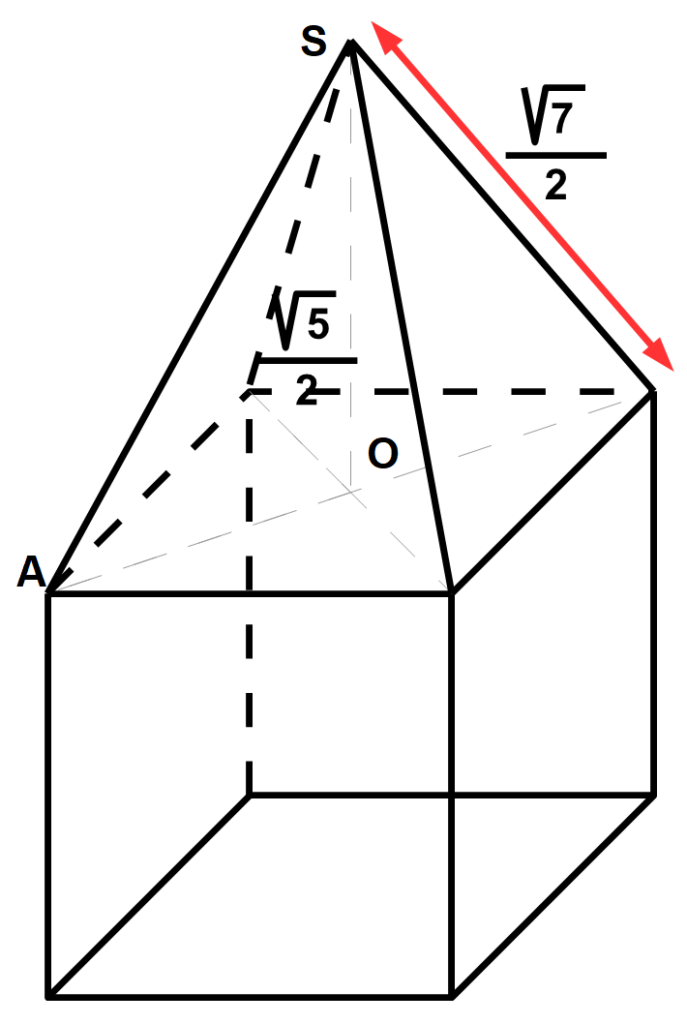
Si on donne à la hauteur une mesure égale à la moitié de racine de 5 l’arête du pyramidion est égale à la moitié de racine de sept.
Cette particularité de la pierre cubique à pointe est peut-être l’explication géométrique de sa présence dans nos temples.
Il est encore une pierre cubique remarquable à signaler, c’est celle dont les quatre faces du pyramidion sont les quatre cinquièmes d’un pentagone. L’angle au sommet de chaque face est donc de 72° et les angles à la base sont de 56°.
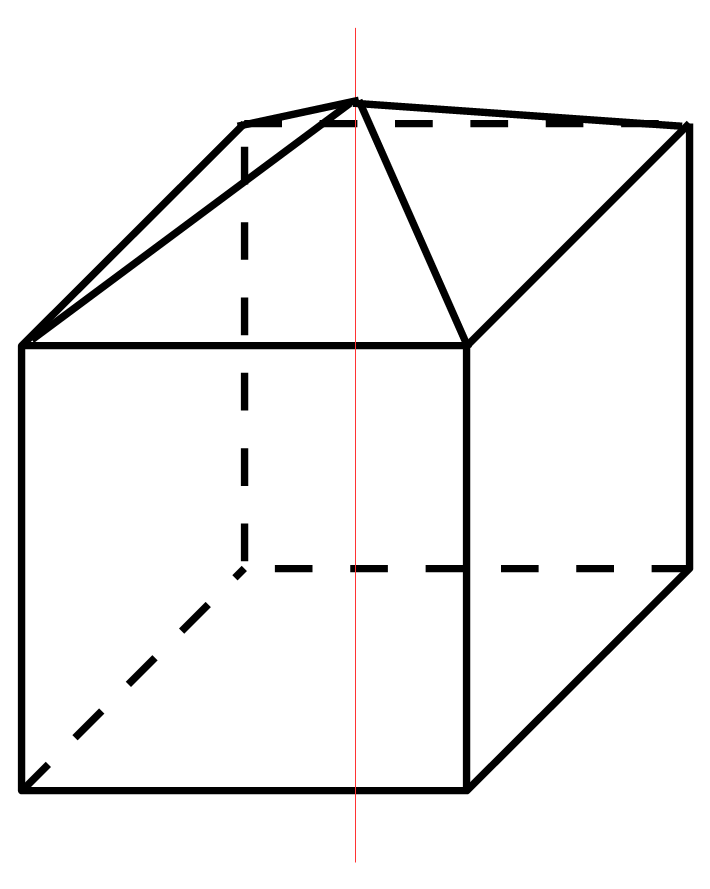
Voici une image en perspective de cette pierre cubique à pointe.
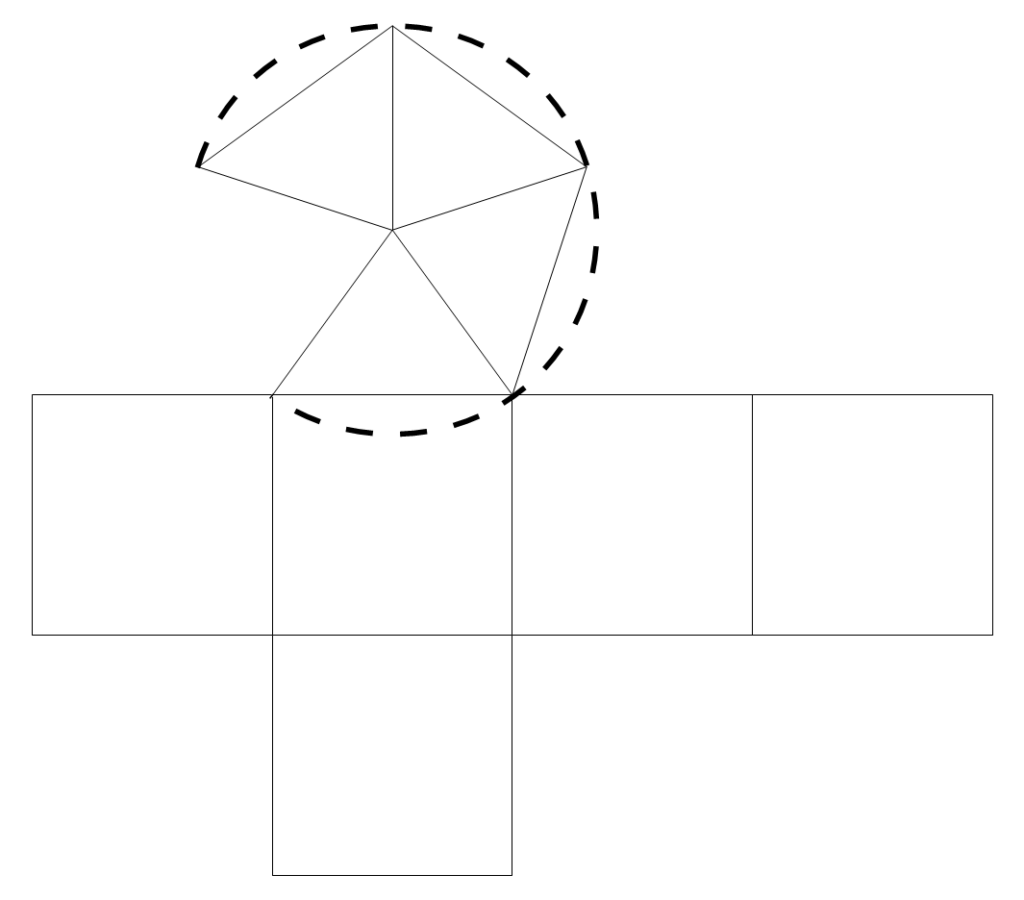
Nous avons joint à l’image de cette pierre celle de son développement (qui avait été donné dans l’un des cahiers de Boscodon comme épure du toit à quatre pans.
La pointe du pyramidion est à une distance des angles de la pierre cubique égale au côté du cube de base.
Dans ce cas, chaque face du pyramidion est un triangle régulier (isocèle). Il en résulte que l’arête du pyramidion est égale à 1 et son carré à 1 (4/4), la demi diagonale de sa base est égale à racine de deux sur deux et son carré à 2/4. La hauteur du pyramidion est donc égale à ½ (4/4 – 2/4 = 2/4 et la racine 2/4 soit 1/ 2 et la racine de ½ est égale à Racine de 2 sur 2). Quant à l’apothème SM SO est égal à Racine de 2 sur 2 et OM est égal à ½ le carré de racine de 2 sur 2 étant égal à 2 / 4 et celui de ½ à ¼ la somme de ces deux carrés est égale à 3 / 4 et l’apothème à Racine de 3 sur deux.
La pierre cubique développée
La pierre cubique a pointe à neuf faces : cinq carrées et quatre triangulaires. La façon la plus simple de représenter son développement est donc une croix a branches égales, chacune se terminant par une pointe.
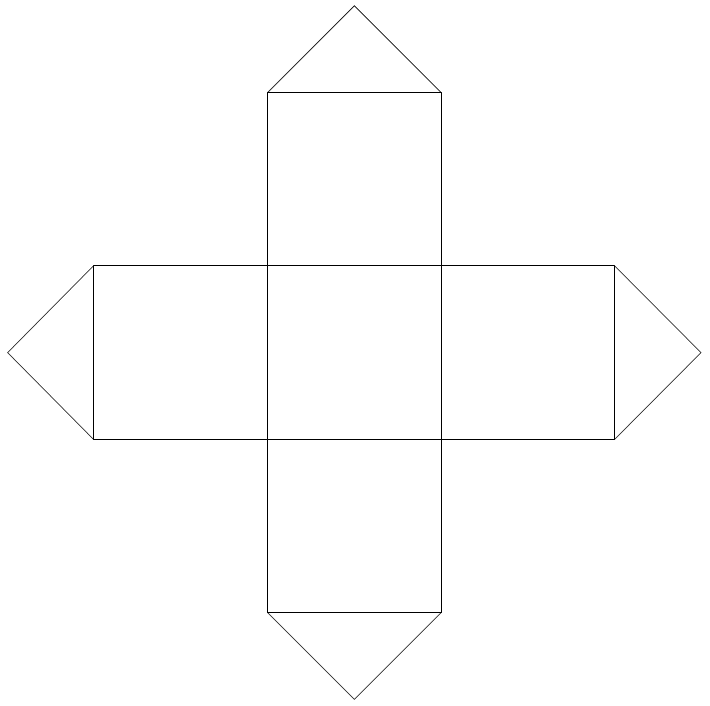
L’image de ce développé est une croix divisée en cinq parties. Les quatre carrés périphériques peuvent être considérés comme quatre régions du monde sensible correspondant aux quatre points cardinaux et aux quatre éléments, représentés par les quatre triangles. Il ne faut pas déclarer d’orientation définitive d’une telle croix et encore moins assigner à chaque pointe une correspondance définitive avec l’un des quatre éléments, parce que ces correspondances varient suivant le contexte. Par exemple, si on se trouve dans un contexte paysan ou agricole et dans l’hémisphère Nord, on pourra légitimement assigner le Feu au Midi, parce que c’est de ce point cardinal que le soleil se rapproche le plus en Été. Le même raisonnement conduit à assigner cet élément au Nord si on se trouve dans l’hémisphère Sud.
Cependant si on considère le mouvement du soleil en trois dimensions, force est de remarquer qu’en été il atteint le tropique du cancer et se trouve donc bien plus haut dans le ciel qu’en hiver et bien plus proche du pôle Nord. Ce raisonnement conduira donc à attribuer le feu au Nord si on se trouve dans l’hémisphère Nord.
Cet exemple simple montre pourquoi il faut se méfier de toute liste de correspondances formelle, comme aiment tant en établir certains auteurs.
Quant au carré central, c’est évidemment l’interface symbolique avec le monde invisible où il n’y a plus « ni temps, ni espace ni aucun changement d’aucune sorte ». C’est le point ou l’unité qui sont inconnaissables. Mais pas seulement ! Si la croix est verticale la pointe du haut est une « antenne » pointée vers la transcendance : ce qui est au-delà du monde sensible (que les croyants appellent souvent « le Ciel » sans savoir trop d’ailleurs ce qu’ils désignent par ce terme). La pointe inférieure est une autre « antenne » qui reçoit les influences chtoniennes quant aux pointes latérales elles assurent le contact avec le monde sensible. Enfin dans ce cas le carré central est le cœur : le centre de l’être qui est la porte de son monde intérieur qui est aussi comme l’au delà du sensible et comme l’au delà du centre, l’unique monde invisible.
Évidemment ce n’est là encore qu’une façon de comprendre le symbole de la pierre cubique à pointe développée et cette explication doit être pour le lecteur non une limite mais un marche-pied pour aller au-delà.
On remarquera que ce symbolisme de la pierre développée s’applique également à la pierre elle-même dont la face inférieure est au contact du sol et dont, dans les meilleures conditions nos sens ne nous révèlent que cinq faces (3 triangulaires et deux carrées). Il faut observer aussi que sa pointe, comme celle des obélisques est censée toucher la voûte céleste, parce qu’en principe son sommet est un point.
La pierre cubique à pointe et les nombres entiers
La pierre cubique à pointe et le nombre 26
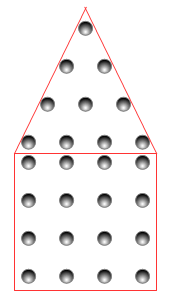
Dans son ouvrage les symboles de la science sacrée René Guenon explique la pierre cubique par le schéma ci-contre. Nous ne doutons pas du fait que ce schéma soit une des explications traditionnelles de la présence d’une pierre cubique à pointe dans les loges. Nous n’en doutons pas, bien que la répétition du rang de quatre points, à la fois dernier rang d’une face triangulaire et premier d’une face carrée nous semble quelque peu abusive… Mais cela peut être une façon comme une autre de cacher le nombre vingt-deux qui est celui des lettres hébraïques. Comment mieux cacher un nombre clé qu’en utilisant un autre nombre clé pour le dissimuler.
La pierre cubique à pointe en nombres figurés
Si nous considérons une pierre cubique sans doublement du rang de quatre points, nous pouvons l’imaginer comme la superposition d’une pyramide à base carrée et d’un cube.
Il s’agit donc du cube de 4 (64 points) auquel s’ajoute la pyramide d’ordre 4 et de rang 3.
Comme nous savons :
D’autre part que la pyramide d’ordre o et de rang r est égale à La pyramide de rang r et d’ordre 3 à laquelle on ajoute o – 3 fois la pyramide d’ordre 3 de rang r-1 ;
Il nous est facile de calculer la pyramide d’ordre 4 et de rang 3
La pyramide d’ordre 3 de rang 3 c’est : 1 + 3 + 6 soit 10
Celle de rang 2 c’est : 1 + 3 soit 4
La pyramide de rang 3 et d’ordre 4 vaut donc 14
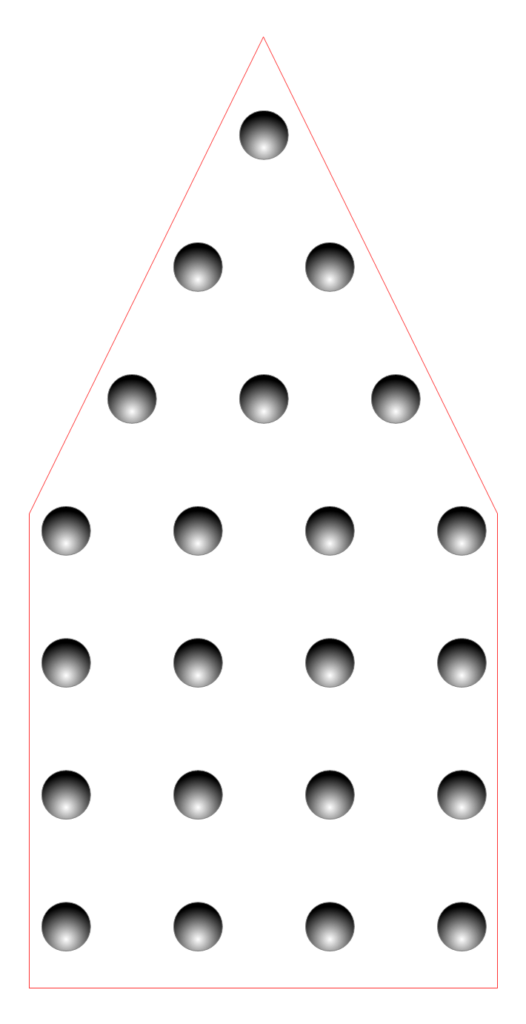
Notre pierre cubique à pointe représentée comme un nombre figuré à 3 dimensions vaut donc 78 (64 + 14) … Le nombre de générations d’Elohim à Jésus selon Marc (et probablement pour la même raison le nombre d’arcanes du tarot). Remarquons que si nous contemplons une seule face de la pierre les 22 points visibles correspondent au nombre de générations d’Elohim à Abraham.
Ce n’est pas tout ! Les 14 points de la pyramide correspondent aux 14 générations composant un cycle et Luc compte quatre cycles de 14 générations.
Par ailleurs si nous retranchons 22 de 78 nous obtenons 56 qui correspond aux quatre cycles de 14 générations entre Abraham et Jésus et aux 56 arcanes mineures du tarot.
Ces considérations sont-elles légitimes ?
Les anciens bâtisseurs puis les maçons du XVIIIe siècle ont-ils construit la pierre cubique à pointe « en points » comme nous venons de le faire ?
Nous n’en doutons pas leur premier manuel de mathématique, celui dans lequel ils apprennent à compter, c’est l’Institution arithmétique de Boèce. Les nombres figurés pythagoriciens leurs sont donc aussi familiers qu’à nous l’addition, la multiplication et la division. On devrait même envisager que c’est à partir de ce modèle en points qu’ils ont décidé d’installer ce symbole dans leurs loges. A noter que cette pierre cubique à pointe semble être une exclusivité continentale.
L’utilité de ces pierres
Nous l’avons déjà écrit ces deux pierres, d’après les instructions par questions et réponse ont un même usage : « Elles servent aux compagnons à aiguiser leurs outils ». Rien qu’en les regardant, l’une comme l’autre semble totalement inadaptées à cet usage, d’autant que le symbole veut que les compagnons qui participent à la construction du Temple de Salomon soient des ouvriers d’élite. Des experts en taille et en assemblage des pierre ainsi qu’en géométrie. Or de bons ouvriers ont toujours de bons outils ! Il en résulte que soit les instructions par questions et réponses ont été falsifiées au cours des temps, soit le verbe aiguiser est un mot substitué qui fait allusion à un autre verbe.
C’est uniquement la chance qui nous a permis d’élucider ce mystère. La clé est dans les dictionnaires du XVIe et du XVIIIe siècle…
Jusqu’au XVIe siècle inclus le verbe affuter signifie préparer un outil ou autre chose. Ainsi, le Trésor de la langue française donne cet exemple : « Belzébuth, (…) s’était fait ce raisonnement triomphal qu’il serait difficile de lui tirer les oreilles puisqu’il n’en possédait pas, et qu’on ne pourrait se livrer sur lui à cette plaisanterie vulgaire de lui affûter une casserole au derrière, puisque la queue absente interdisait ce genre de facétie… T. Gautier, Le Capitaine Fracasse,1863, p. 31. » De même en artillerie on dit (peut-être on disait) « affuter les canons » car ils sont fixés à un « affut » et c’est la position de cet affut qui va leur permettre de tirer dans telle direction plutôt que dans telle autre.
Cependant des le XVIIe siècle le sens premier d’affûter est devenu synonyme d’aiguiser. De même l’expression affûter les canons est tombé en désuétude (au profit de « mettre en batterie ») selon le Littré de 1873 – 1874. Quant au « Dictionnaire françois latin » plus connu sous le nom de dictionnaire de Trévoux et très populaire au XVIIIe siècle il donne ces définitions :
« AFFUTER, v. a. Disposer le canon à tirer, le mettre en mire. Tormentum ad emissionem disponere librare.
Affûter, signifie aussi chez les ouvriers, aiguiser les outils. Acuere, exacuere.
Les Peintres & les Dessinateurs disent aussi affûter les crayons ; pour dire, aiguiser les crayons. »
Affûter, se dit mieux des bois ou des crayons que des métaux. On aiguise un instrument neuf, & celui qui a servi : on n’affûte que celui qui a servi. Aiguiser, c’est donner la forme convenable à l’extrémité d’un instrument qui doit être pointu. Affûter c’est réparer cette forme altérée par l’usage. »
En clair, pour comprendre vraiment ce que lui racontent les instructions par questions et réponses, le compagnon maçon doit se référer à des sens et des usages datant de deux siècles plus tôt.
Le Rite Écossai Rectifié donne néanmoins une piste aux compagnons. Ce rite en effet associe à chaque grade un tableau symbolique qui est placé à l’Orient, généralement au pied de la table du Vénérable Maître. Celui du grade de compagnon représente une pierre cubique sur laquelle est posée une équerre. L’équerre est posée en oblique. Curieusement, ce rite qui ne revendique guère des origines opératives, tout comme ne les revendiquaient pas celui de la Stricte Observance Templière, qui lui a transmis ces « symboles du grade » propose avec cette pierre une véritable clé opérative.
En effet l’image s’accompagne d’une devise : dirigit obliqua que l’on traduit par dirige-la en oblique, or c’est exactement de cette façon que s’utilise l’équerre. En effet avec l’équerre placée ainsi en oblique l’ouvrier vérifie à la fois l’équerrage des deux faces de la pierre et le surfaçage de l’une d’elle. Avec cette équerre on retrouve le sens premier d’affuter : préparer un outil, le mettre au point. En effet, dans le passé, les opératifs, fabriquaient eux-mêmes leurs outils. De même, face a des rituels où chaque phrase est une énigme en présence d’objets symboliques qui tous cachent et révèlent une vérité le maçon opératif se doit d’affuter son esprit, de développer son sens critique, son intuition et sa perspicacité. Dirigit obliqua !
C’est certes une référence au bon usage de l’équerre, mais cela fait également référence à la « pensée oblique » un terme très en l’honneur au XVIIIe siècle qui désignait à l’époques, entre autres choses la pensée analogique, mais aussi un certain art de regarder la réalité d’un œil différent , celui qui regarde la chose que peut-être certains ont caché derrière ce que l’on voit. Peut-être, car il est possible que personne, du moins aucun être humain ait voulu cacher ou révéler quelque chose consciemment. Cela importe peu, ce qui importe c’est que ce que nous voyons et que ce que nous comprenons grâce à la pensée oblique soit une réalité.
Conclusion
Dans la pensée maçonnique la pierre cubique à pointe reste fondamentalement une pierre cubique. L’adjonction de la pointe permet de la relier non seulement au christ mais aussi à sa généalogie, rappelant à chacun que les maçons du XVIIIe siècle étaient tous de culture chrétienne, même si quelques uns d’entre eux pouvaient faire profession d’athéisme ou être de religion juive. Evidemment, ce n’est certainement pas là la seule raison de l’introduction de cette pierre dans nos temples et nous pensons qu’il faut voir un rapport entre elle et le clocher des églises romanes qui se compose souvent dans certaines régions d’un cube surmontant une tour carrée coiffé d’un toit à quatre pans plus ou moins pentu… Evidemment étant donnée la diversité des édifices qualifiés de « romans » cela ne s’applique que dans certaines régions. On trouve beaucoup de clochers de ce type près des Pyrénées, dans les pays de Loire et dans le Morvan. En revanche en Bourgogne et dans d’autres régions c’est un édifice rare…
Quelques images.
Il faut remarquer sur cette image la bordure de pierres qui marque la base d’un cube probablement approximatif.
Nous constaterons la même démarche sur les quatre autres exemples.
La végétation laisse penser que cette église est en zone méditerranéenne. Le toit est bien moins pentu, mais la base du cube est toujours représentée sur la muraille.
E pour éviter les doutes inutiles voilà trois autres exemples.
