Le Delta : symbolisme pythagoricien

Les Old charges en témoignent : pour les opératifs, Géométrie et Maçonnerie sont synonymes et elles évoquent tantôt Pythagore, tantôt Euclide, comme l’un des fondateurs du métier qui enseigna la maçonnerie aux Égyptiens.

Les maçons, même les spéculatifs, reçoivent avec leur initiation une filiation pythagoricienne. Le Delta placé à l’orient en témoigne… Et ce n’est là que le premier témoignage que rencontre le maçon spéculatif.

Malheureusement, la culture contemporaine est très éloignée du pythagorisme qui n’est rien d’autre qu’une « métaphysique des nombres et des figures géométriques ».  Il en résulte que cet aspect du symbolisme est souvent, non pas négligé, mais ignoré. Il est même, par certains, considéré comme sans intérêt…

Digression nécessaire : Nombres, figures, symboles

Les nombres sont des idées abstraites, les figures sont la traduction ou plutôt la manifestation de ces idées dans le monde intermédiaire « dit de la création » : le monde où est conçue l’idée d’espace et de forme, mais où il n’existe encore ni espace ni forme…  Ce sont donc des « objets de l’esprit »

Les figures géométriques sont imparfaitement reproduites dans le monde créé celui où existent l’espace et la matière : Il ne peut y avoir dans le monde créé ni point, ni droite, ni cercle, ni aucune figure géométrique. Il n’existe dans le monde créé que des représentations imparfaites de ces figures qui sont comme les nombres : des vues de l’esprit.

En témoigne la définition du point donnée par Euclide dans ses Éléments de géométrie [1]:

« Les physiciens disent que le point est le moindre objet de la vue et que celui-ci peut être [dessiné] avec [de l’] encre ou autre chose » Voilà selon Euclide la définition, non du point, mais de sa représentation dans le monde matériel.

« Mais les mathématiciens, rejetant cette définition disent que le point est un objet de l’intellect si subtil qu’il ne peut être divisé en aucune partie : Et ce dernier ne se peut écrire [dessiner] mais seulement entendre et imaginer »

En clair, le point est un concept qui ne peut exister dans le monde matériel. Euclide ajoute aussitôt que « pour le représenter à nos sens extérieurs » nous nous servons du « point physique ».

Puis il revient au concept de point (au point du mathématicien) en précisant que celui-ci n’a aucune dimension (ni longueur ni largeur ni épaisseur) mais est le principe de toutes les dimensions.

Cette distinction entre le « point concept » et son imparfaitereprésentation matériellequ’Euclide nomme le « point physique » est essentielle pour comprendre le symbolisme des figures.

Par ailleurs, avant d’aller plus loin, il faut savoir que les auteurs pythagoriciens ne se préoccupaient que des concepts et témoignaient d’un profond mépris pour les mathématiques appliquées (leurs mathématiques étaient en réalité une métaphysique). Cependant nous traitons de symbolisme maçonnique et la Maçonnerie, fusse-t-elle spéculative est l’héritière (au moins spirituellement) d’une maçonnerie, qui pour bâtir, utilisait les mathématiques appliquées, ce qui a influencé la nature et le sens des symboles maçonniques. Nous serons, pour cette raison (et parce que les mathématiques qu’on enseigne de nos jours sont orientées sur la pratique) contraints d’envisager les propriétés particulières des représentations matérielles des figures géométriques. Pour cela nous emprunterons à René Guenon la notion d’unité minimum absolue de distance[2] dont l’existence dans le monde matériel est une conséquence directe de la double définition du point donnée par Euclide.

Le point matériel (physique) est donc, pour nous, Francs-maçons, un symbole : la représentation d’un concept universel « le point du mathématicien ».

Il représente le point mathématique, ce dernier étant lui-même l’image idéale de L’unité. L’Unité mathématique, qui, comme le point géométrique, ne peut être divisée[3].

Cette Unité relève de l’arithmétique, mais ces deux aspects des mathématiques sont tellement liés qu’Euclide consacre la totalité de son septième livre a l’exposé de l’arithmétique.

Les termes monde de la création et monde créé que nous avons employé dans cette introduction étaient certes pratiques adaptés à notre explication, mais ne correspondent pas aux concepts qui seront utilisés par la suite. Nous devrons en effet employer les termes :

« Monde des idées » ou des concepts et « Monde sensible »

Le « Monde sensible » englobant toutes les « choses et êtres, phénomènes » qui sont perceptibles aux sens.

Le « Monde des idées » englobant tout le reste dont, entre autres, nos pensées.

Fin de la digression

Le Delta : un symbole.

Que les travaux maçonniques soient ouverts au nom du G. A. D. L. U, de l’Humanité ou de quoi que ce soit d’autre, le Delta Lumineux est à l’Orient.

Aspect physique

C’est un delta, donc la lettre grecque majuscule du même nom qui a la forme d’un triangle isocèle qui est (en typographie) presque un triangle régulier (équilatéral[4]).  Pourquoi « presque » ? Parce que la perfection n’est pas de ce monde et que notre delta est matériel. Dans le dessin de la lettre grecque cette imperfection est volontairement perceptible. Quant au delta de l’orient c’est un triangle régulier… mais forcément imparfait puisque matériel.

Tout triangle fusse-il lumineux qui ne présenterait pas à l’œil l’image d’un triangle régulier (qui est le concept du delta) ne pourrait être appelé « Delta ». Nous reviendrons marginalement sur cette question.

Sens

Pour ceux qui utilisent ce terme, le Delta représente « la première manifestation du Grand Architecte de L’univers ». Pour les autres, il représente forcément quelque chose d’équivalent un « commencement des choses » parce que le triangle est la plus simple et le principe de toute surface.

Le delta et le point physique

Le point du mathématicien (ou du métaphysicien) est un objet de l’intellect. Sa représentation dans le monde sensible est le point physique qui a des dimensions (certes minimales) et une forme.

Le dessinateur qui veut déterminer un point, trace l’intersection de deux lignes. Le typographe, qui veut représenter un point utilise l’image d’un cercle assez petit pour représenter le « point physique ». Nous devons donc observer que le point du typographe n’a pas la même forme que le point du dessinateur. Cette réalité étant constatée, il devient légitime de se poser cette question :

Quelle serait la forme symbolique idéale du point matériel pour qu’il représente le point du physicien ?

Étant matériel notre représentation devrait avoir une surface aussi petite que possible. Il en résulte que la représentation idéale du point du physicien (le moindre objet de la vue) serait le triangle tracé en joignant trois points mathématiques assez distants les uns des autres pour que la surface triangulaire obtenue soit visible.

Autrement dit, il faudrait commencer par déterminer trois points juste assez éloignés les uns des autres pour que l’espace entre eux puisse être vu par l’observateur puis joindre les trois points…. Comme l’acuité de la vue de l’observateur est variable, cette représentation est un pur concept.

En revanche ce raisonnement peut et même doit nous conduire à affirmer que le delta lumineux à l’orient, étant la représentation démesurément agrandie, du point du physicien, symbolise (entre autres choses) le point mathématique et par conséquent l’unité mathématique.

De ce fait, il symbolise également l’Un. Le point central l’unité métaphysique.

Le delta : un triangle régulier.

C’est donc une figure composée de trois points reliés entre eux par des segments de droite. Comme son nom l’indique le triangle se relie au ternaire….

Remarquons que du point de vue des anciens, tout triangle « non régulier » est un triangle déformé ou imparfait.

Le delta : une lettre grecque

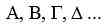
Telles sont les quatre premières lettres de l’alphabet grec. Le delta est la quatrième lettre et représente le nombre quatre. Il en est de-même de notre delta à l’Orient, parce que le delta est l’initiale de Zeus en grec, de Dia (dieu en dorique) qui donne Deus en Latin et Dio en italien… Il s’agit bien entendu de ce que les Églises chrétiennes appellent « Dieu le Père ».

Mais pourquoi le delta triangulaire représente-t-il le quatre ?

Avant d’aller plus loin considérons la forme des lettres grecques

A se compose de trois traits qui mettent en valeur un minuscule triangle… Deux côtés de ce triangle, prolongés laissent penser qu’il pourrait croître.

B entoure deux surfaces suggérant une dualité. On pourrait penser que ces surfaces signalent à l’observateur la proximité de deux points géométriques.

G, le Gamma a la forme d’une équerre, deux droites perpendiculaires joignent trois points[5].

Le D est un triangle. C’est la première figure fermée, il délimite une aire mesurable, mais ne comporte toujours que trois points… Il a pour valeur quatre mais symbolise à la fois : le UN (le point), le trois, et le dix qui est l’unité de second rang.

Comment le delta peut-il symboliser tant de nombre

La clé qui permet de le comprendre est l’arithmétique de la Grèce ancienne (empruntée à l’Égypte et à Babylone qui l’avaient eux-mêmes emprunté à L’Inde). En un mot l’arithmétique antique.

Les nombres y sont représentés par des points.

. représente le 1, : représentent le 2, \représente le 3.

1 n’est pas un nombre, mais le principe de l’imparité. Ce n’est pas un nombre parce qu’il ne répond pas à la définition antique du nombre impair : Un nombre impair peut être divisé en deux parties inégales ». Or, par définition l’unité ne peut pas être divisé.

2 n’est pas, non plus, un nombre, parce qu’il ne répond ni à la définition antique du nombre pair ni à celle du nombre impair et qu’il n’existe que deux sortes de nombres : les pairs et les impairs. « Définition du nombre pair « Un nombre pair peut être divisé en deux parties égales ou en deux parties inégales ». Deux est le principe de la parité. (quatre est le premier nombre pair : on peut le diviser en deux parties égales – 2 + 2 = 4 et en deux parties inégales – 3 + 1 = 4.

3 est le premier nombre et le premier impair (on ne peut le diviser qu’en deux parties inégales) : 2 + 1 = 3.

4 est le 2^e nombre et le premier nombre pair (on peut le diviser en deux parties égales (2 + 2 = 4) et en deux parties inégales (3 + 1 = 4).

Ces principes étant posés, arrivons-en à la clé : les nombres triangulaires.

Le symbolisme du delta par les triangulaires

Définition : Le triangulaire (ou triangle) de rang r est la somme des nombres de 1 à r

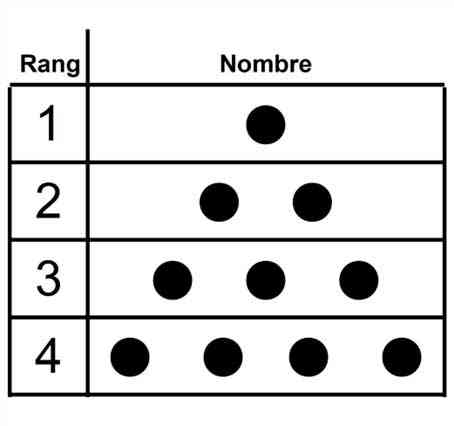
De cette définition, il résulte que pour tracer le triangle de rang 1, nous dessinons 1 point sur la première ligne. Le triangle de rang 1 est 1.

Pour tracer le triangle de rang 2, nous dessinons 2 points sur la seconde ligne. Le triangle de rang 2 est 1 + 2 = 3.

Pour tracer le triangle de rang 3, nous dessinons 3 points sur la troisième ligne. Le triangle de rang 3 est 1 + 2 + 3 = 6.

Pour tracer le triangle de rang 4, nous dessinons 4 points sur la quatrième ligne. Le triangle de rang 4 est 1 + 2 + 3 + 4 = 10.

Notre delta situé à l’Orient symbolise l’Unité parce que la représentation du point la plus parfaite est triangulaire (voir ci-avant).

Pour la même raison, il symbolise le trois : parce que le triangle est la première manifestation spatiale possible (dans un espace à deux dimensions[6]).

Parce que la lettre Delta vaut 4, il vaut quatre… et symbolise aussi le 4 d’ailleurs :

• Étant triangle régulier il peut être inscrit dans un cercle et le centre de ce cercle est alors également le centre du triangle. Il comporte donc trois points visibles plus un point invisible soit quatre points.
• Le triangle régulier est la projection sur le plan du solide appelé tétraèdre, solide qui a quatre sommets et quatre faces triangulaires… Il comporte donc trois points visibles plus un point invisible soit quatre points (trois dans le plan et un hors du plan). C’est la première manifestation possible dans un espace à trois dimensions.

Cependant, le tétraèdre est peu utilisé en architecture et, quand le pythagoricien pense tétraèdre (pyramide à base triangulaire), le maçon pense pyramide ou pyramidion.

Le tétraèdre a quatre sommet, et quatre est le nombre pyramidal d’ordre 3 de rang 2 : le premier qui puisse représenter un volume. Le tétraèdre est un triangle à 3 dimensions

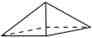
La pyramide a base carrée (ou le pyramidion) qui a cinq sommets, est le pyramidal d’ordre 4 de rang 2 …

Un pyramidal d’ordre o de rang r est égal au pyramidal d’ordre 3 de rang r auquel on ajoute, o-3 fois, le pyramidal d’ordre 3 de rang r-1. Quant au pyramidal d’ordre 3 de rang r, c’est la sommes des triangles de 1 à r (tout comme le triangle est la somme des nombres de 1 à r).

La pyramide a base carrée est un carré à 3 dimensions.

Enfin il symbolise la dizaine, parce que le triangle de rang quatre vaut 10 et parce que 10 est l’unité de second rang (voir la représentation des nombres sur l’abaque ci-avant).

Parce qu’il symbolise à la fois l’unité de rang 1 et l’unité de rang 2 on doit le considérer comme le symbole de toutes les unités de rang impair et pair. : unités, dizaines, centaines, milliers …

On doit également considérer qu’à ce titre il est symbole de la totalité. En effet, la totalité est semblable à l’unité, parce qu’elle est indivisible : la totalité divisée cesse d’être la totalité.

Délire ? Élucubrations ? Certainement pas ! ces aspects symboliques du triangle sont validés à la fois par l’arithmétique et par la géométrie.

Le triangle en arithmétique et en géométrie

Tout nombre entier plus grand que 3 est une somme de triangulaire :

Quatre (le carré de deux) est la somme du triangle de rang 1 (1) et du triangle de rang 2 (3). Cela vaut pour tous les carrés ! le carré du nombre n est égal à n x par n ou à la somme du triangle de rang n et du triangle de rang n-1 par exemple 9, carré de 3 est la somme du triangle de rang 3 (6) et du triangle de rang 2 (3).

Cinq est la somme du triangle de rang 2 (3) et de deux fois le triangle de rang 1 (1). Ce nombre est le prototype des nombres dits pentagonaux (ou pentagone). Le pentagone de rang n est égal à la somme du triangle de rang n et de deux fois le triangle de rang n-1.

Et ainsi de suite…

Ainsi si nous appelons « ordre » le nombre de sommet d’un polygone nous pouvons écrire :

Le polygonal d’ordre o et de rang 1, vaut 1.

Le polygonal de d’ordre o et de rang 2 vaut o.

Le polygonal d’ordre o et de rang n vaut la somme du triangle d’ordre n et de o-3 fois le triangle de rang n-1.

Ainsi 153, le nombre de poissons pêchés par les disciples du Christ peut être ainsi calculé :

le nombre 153 est :
Polygone d’ordre 153 de rang 2.

• Il peut être calculé comme :
  Polygone d’ordre 52 de rang 3
  Soit le triangle de 3 (6) + 49 fois le triangle de 2 (3) → 6 + (49 x 3),
   donc : 6 + 147 = 153[7].
  Polygone d’ordre 6 de rang 9
  Soit le triangle de 9 (45) + 3 fois le triangle de 8 (36) → 45 + (36 x3),
  donc : 45 + 108 = 153.
• Polygone d’ordre 3 de rang 17 :
  La somme des nombres de 1 à 17 ou selon la formule de calcul rapide :
   17 x 18 / 2 = 153.

Toute surface polygonale est une somme de triangles

Donc toute surface polygonale peut être pavée avec des triangles d’une ou de plusieurs façons. Ici un petit dessin sera plus parlant qu’un long exposé.

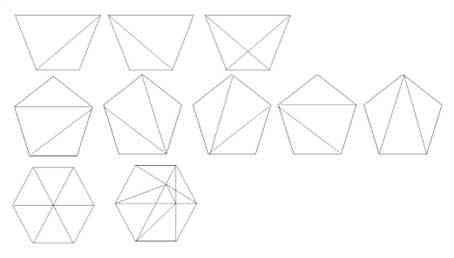
Ainsi tout nombre et tout polygone est composé de triangles. Par ailleurs, dans le monde sensible la courbe n’existe pas, et ne peut exister en raison de l’existence d’une unité minimum absolue de distance en deçà de laquelle deux points matériels sont confondus. Il en résulte que dans le monde sensible le « cercle » est une approximation : un polygone avec un nombre indéfini de côtés…

Revenons donc à notre delta en tant que symbole du point primordial, de la première manifestation de l’espace.

Il est évidemment ; de la même façon la plus petite surface que l’on puisse dessiner.

Pourquoi le delta est-il souvent représenté dans un cercle ?

Souvent ce cercle est un cercle de nuages, il existe une explication astronomique qui justifie cette représentation. Cela dit, cette représentation se justifie mathématiquement. Considérons notre point primordial.

Les trois sommets d’un triangle représentant le point primordial sont, puisqu’il est le moindre objet de la vue, séparés d’une distance inférieure ou égale à l’unité minimum absolue de distance. Le triangle étant inscriptible dans un cercle et un seul on peut en conclure que les trois sommets du triangle sont situés sur un cercle dont le rayon est (c x √3)⁄ et sa circonférence mesure c x 2√3 x pi.

Donc le tiers de la circonférence est un nombre inférieur à deux. Entre deux sommets du triangle, aucun point situé sur le cercle exinscrit ne peut donc être figuré. En voici la démonstration graphique. L’unité minimum absolue de distance est appelée u.

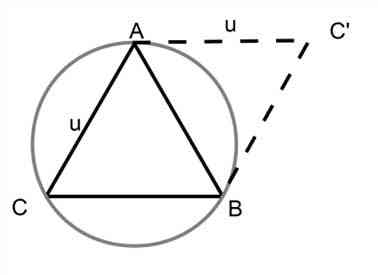
Sur notre schéma, le centre n’apparait pas. Il se situe à moins d’une unité minimum absolue de distance des points A B et C. C’est donc un point géométrique, mais ce ne peut être un point des physiciens. Si nous appelons ce centre O, les points A B et C matérialisent physiquement le « lieu géométrique des points (du physicien) équidistants du point O[8] » … Il en résulte que notre plus petit triangle matériel possible est aussi le plus petit cercle matériel possible.

Au-delà du delta…

En revanche dans un cercle de diamètre deux u, On peut placer un triangle qui soit le reflet du premier. On obtient un hexagone étoilé dont les sommets sont distants de u. Les six sommets de l’hexagone, sont les seuls points matériels qui peuvent être placés sur la circonférence du cercle.

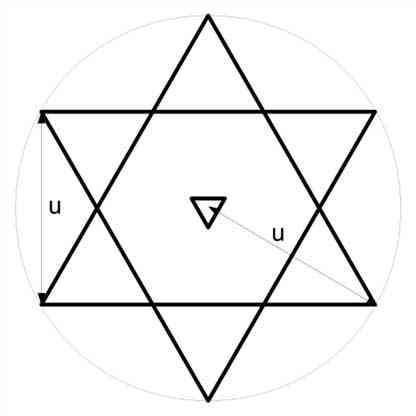
Le centre est ici figuré par un triangle pointe en bas, comme dans la tradition tantrique.

Définition du cercle par Euclide :
« Le cercle est une figure plane contenue par une seule ligne qu’on appelle circonférence vers laquelle toutes les lignes droites menée du d’un seul point de ceux qui sont en icelle figure sont égales entre-elles.
Et ce point est appelé centre. »  

Résumé : Le Delta a l’Orient représente l’unité, le point matériel, donc la première manifestation du créateur dans le monde des idées puis dans le monde matériel. Comme il représente l’unité, il symbolise aussi la totalité. Parce que tous les nombres sauf 3 sont des « sommes de triangles (nombres triangulaires) et parce que toutes les figures polygonales sont des sommes de triangles, il est la clé de la compréhension des nombres et des formes.

[1] Les quinze livres des éléments géométriques d’Euclide Paris 1632 – disponible sur Google Books. Cette traduction a l’avantage de ne pas être commentée par un mathématicien contemporain.

[2] Voir Le symbolisme de la croix et Les principes du calcul infinitésimal qui, contrairement à ce que son titre laisse penser est un ouvrage de métaphysique.

[3] Du point de vue métaphysique et symbolique les nombres décimaux doivent être considérés comme un artifice de calcul ou d’écriture et relèvent du quantitatif quand l’unité et les nombres évoqués ici relèvent du qualitatif.

[4] C’est la même chose ! Le triangle équilatéral que j’avais étudié à l’école primaire est devenu un triangle régulier quand je suis entré au collège.

[5] Je ne sais pas si ces observations symboliques répondent à une quelconque tradition, mais elles semblent correctes pour les quatre premières lettres majuscules… Pour les suivantes, je ne sais pas

[6] Trois est aussi, le premier nombre pouvant exprimer une aire et donc le premier nombre à deux dimensions (aire du triangle de base 2 et de hauteur 3 – ou demi  aire du rectangle de 2 sur 3).

[7] Nous utilisons pour ces calculs la formule Tr = r(r+1) / 2 qui est plus rapide qu’une somme de 1 à n.

[8] Cette définition moderne est incorrecte du point de vue pythagoricien, car selon Euclide la ligne du mathématicien est « une longueur sans épaisseur ». Elle ne saurait être composée de points, mais c’est, comme lui, un « objet de l’esprit ».