« Et puisqu’un dieu me fait parler, j’obéirai religieusement à ce dieu qui dicte mes paroles ; j’étalerai au grand jour les secrets de ce Delphes qui est en moi, ceux du ciel même, et je dévoilerai les oracles de l’ultime sagesse. Je proclamerai les grands mystères que le génie de nul homme avant nous ne put pénétrer, et qui restèrent longtemps cachés. » (Les Métamorphoses, Livre XV, Vers 131-167)
Vers le 6ème siècle avant J.-C., en Égypte ancienne, les nombres ne codaient encore que les impôts, le commerce, les salaires. L’évaluation, par les harpédonaptes (fonctionnaires royaux, arpenteurs géomètres), de la surface des champs cultivables dont la crue du Nil a effacé les bornes limitatives, ne géométrise pas, mais ne cherche qu’à clore les contentieux entre voisins par la force de l’État. Avec le droit de propriété, voici du droit civil et privé. Mais aussi, en délimitant les bornes, le cadastre royal fixe l’assiette de l’impôt. Voilà du droit public et fiscal. Les nombres ne disent, ainsi, que les relations humaines.
Et puis un jour… De la gigantesque masse de pierres, du mausolée du pharaon Kéops va naître la géométrie sur le sable ensoleillé maquillé par son ombre. En rapportant l’ombre du tombeau à celle d’un poteau de référence, ou à la mesure de son corps, selon la légende, Thalès énonce l’invariance d’une forme malgré la variation de sa taille. En effet, son théorème montre la progression ou la régression infinie de la dimension, dans la conservation d’un même rapport, du colossal, la pyramide, au plus médiocre bâton planté dans le sol. Quel effacement de toute hiérarchie dans le semblable, puisque chaque stade, du plus grand au plus petit, conserve le même rapport.
Thalès nous fait découvrir[1] ainsi un monde hors des sociétés où les choses sont en rapport avec elles-mêmes. «La proportion parle, sans bouche humaine, montre un ordre qui ne connaît pas la loi sociale, qui échappe à la toute-puissance. Une liberté, une égalité sans pareilles ! Pharaon meurt une seconde fois quand Thalès, en mesurant la pyramide, la réduit à un simple polyèdre dans l’homothétie de son ombre de géomètre[2].
La proportion analogique, voici la grande conceptualisation grecque, pas celle du rapport simple a/b, mais celle qui intéresse en tant que médiété[3], celle qui va d’un rapport à un autre, tel a/b = c/d et par substitution peut passer de celui-ci à un troisième rapport et ainsi de suite. Il ne s’agit point de couper quelque chose en part, donc de partager ou de prélever, ce que chacun, généreux ou léonin, sait faire depuis les commencements, mais de construire, pas à pas, une chaîne, donc de trouver ce qui, sous-jacent, stable et glissant, transite le long de son enchaînement. Les Grecs appelleront ce rapport d’analogie «logos». Comme Platon et Aristote, les Stoïciens penseront que le logos pur est parole, intelligence, un accès direct et véritable aux choses, ce que les nombres et leurs rapports peuvent enfin faire.
En ce temps-là, vers le 6ème siècle avant J.-C. vivaient aussi Zarathoustra, Lao-Tseu, Bouddha, Confucius, dans les ailleurs de la Perse, de la Chine, de l’Inde.
Ici, en Grèce, vers 530 av. J.-C., à Crotone, justement revenu d’Égypte mais aussi de Perse, d’Inde, de Chaldée, de Thrace, un homme né 40 ans plus tôt à Samos, ramène avec lui des savoirs ancestraux, une sagesse du monde que ses voyages, ses probables rencontres avec ces personnages suscités, ses initiations reçues ont sans aucun doute forgés. Il est probable qu’il fut initié aux mystères, ceux de Thèbes, ceux des Mages chaldéens, aux pratiques orphiques ; il aurait reçu le baptême dans l’Euphrate, aurait été enseigné par le fameux Thalès et purifié par Zoroaste et Bouddha eux-mêmes. De cette appréhension particulière et métissée du monde d’Asie et d’Asie mineure, Pythagore, car c’est de lui qu’il s’agit, le «premier maître universel» comme l’appelait Hegel, en fera une philosophie.. Comme le rapporte Cicéron, c’est Pythagore qui aurait forgé le mot philosophe pour se définir ainsi devant le tyran Léon de Phlionte qui lui demandait qui il était, et comme il l’expliqua, le philosophe est celui qui cherche à découvrir les secrets de la nature de façon désintéressée. Il aurait participé alors à faire basculer la Grèce d’un mode de pensée religieux à un mode de pensée rationnel.
Comme on le comprend, aux conditionnels employés pour évoquer le parcours de Pythagore, il est difficile de démêler, dans la personnalité du philosophe, ce qui relève de la légende merveilleuse de ce que fut sa vie, car nous n’avons de lui aucun ouvrage, mais seulement quelques fragments d’un de ses disciples appelé Philolaos. Même les fameux vers dorés, qui lui sont attribués, sont douteux quant à leur origine. Il nous est même impossible de distinguer l’enseignement du Maître des théories des disciples. Nous ne pouvons parler que du pythagorisme, sans prétendre savoir ce qu’a pensé Pythagore. De plus, la plupart des renseignements qui nous ont été conservés, épars dans un grand nombre d’ouvrages, ne méritent que peu de confiance. Le mot Pythagore ne désignerait même pas un homme, mais une science.
Nous lisons dans le dictionnaire Welsh, d’Owen Pughes :
Pythagoras : explication de l’Univers, Cosmogonie.
Pythagori : expliquer le système de l’Univers (mot composé de pyt, période de temps ; agori, découvrir).
Python : système de l’Univers.
Pythone : une cosmogoniste, une pythonisse.
Pythoni : traité de cosmogonie.
Pythonydd : celui qui systématise le monde.
Pythagore (VIe siècle av .J.C.) dont le nom est la réduction de l’expression «Pitouï Chel Guer» (גר של פיטוי), «la séduction du converti», se serait converti au judaïsme, son nom serait issu de l’araméen.
Pour Céline Renooz, la célèbre misandre belge, les fables inventées sur la prétendue vie d’un homme appelé Pythagore n’ont aucune réalité. Son opinion sera corroborée par Ernest Havet qui disait : «rien de plus connu que ce nom, rien de moins connu que l’homme lui-même» et de rajouter plus loin : «Je ne considère Thalès, Pythagore, que comme des noms représentatifs d’un système scientifique». Ce qui n’empêchera pas des auteurs classiques de faire de Pythagore un personnage historique et ils lui inventeront une biographie. «Est-il rien de plus vrai que la vérité» demande Nikos Kazantzakis et de répondre : «la légende. C’est elle qui donne une immortalité à l’éphémère vérité.»
Pythagore est donc devenu de bonne heure un personnage légendaire. Laissons donc son histoire aux textes de ses disciples, à toute la littérature très abondante que cet extraordinaire personnage ne manqua pas d’inspirer, aux doxographies, ces compilations des textes grecs du début de l’ère chrétienne. Sur ce sujet, on peut citer les vies de Pythagore écrites, une par Diogène Laerce, une autre par Porphyre, la plus connue par Jamblique, vers le IIe siècle. Citons Diogène Laërce à propos de Pythagore : Comme il était jeune et studieux, il quitta sa patrie et fut initié à tous les mystères grecs et barbares. Il gagna donc l’Égypte, quand Polycrate l’eut recommandé par lettre à Amasis, et il apprit la langue du pays. Il alla aussi chez les Chaldéens et les mages. Étant en Crète, il descendit avec Épiménide dans l’antre de l’Ida. Tout comme en Égypte il était allé dans les sanctuaires, il y apprit les secrets concernant les dieux.
Ce qui paraît intéressant de rapporter ici, c’est ce en quoi son savoir, ses connaissances, ses enseignements, qui lui sont attribués, auraient pu influencer la Franc-maçonnerie.
Il y a deux choses à distinguer dans le pythagorisme : une philosophie, c’est-à-dire une explication de l’univers, et une doctrine morale. On retiendra ces deux aspects avec la philosophie des nombres d’une part , l’éthique pythagoricienne d’autre part.
1- La philosophie des nombres
C’est autour de la souveraineté des nombres que l’on peut penser l’apport de Pythagore à la connaissance universelle et le considérer comme une des sources importantes de la Franc-maçonnerie.
Tout d’abord, ce rapprochement paraît licite car, dans l’ancien Manuscrit Cooke conservé à la Bibliothèque Britannique, on peut lire aux paragraphes 281-326 que toute la sagesse antédiluvienne était écrite sur deux grandes colonnes. Après le déluge de Noé, l’une d’elles fut découverte par Pythagore et l’autre par Hermès le Philosophe, qui se consacrèrent à enseigner les textes qui y étaient gravés. Sur le frontispice des Constitutions d’Anderson on retrouve le «théorème de Pythagore» concernant les triangles rectangles, le reconnaissant sans doute comme le père de la géométrie.
Les bâtisseurs médiévaux, quant à eux, transmettront une géométrie sacrée qui remonterait à Pythagore, qui resta vivace jusqu’au XVIe siècle et dont on connaît l’influence dans la Tradition maçonnique.
Qu’en est-il de cette élaboration philosophique d’objets mathématiques et géométriques permettant la contemplation des formes intelligibles, de ces réalités invisibles qui modèlent l’Univers ?
Pour les pythagoriciens, les choses sont nombres, les nombres se trouvent dans les choses, les nombres sont la cause et les principes des choses ou encore les choses sont constituées par les nombres, comme l’exprime Aristote. Les pythagoriciens furent sans doute les premiers à penser que le nombre est la structure d’accueil pour recevoir, analyser et chercher à comprendre l’incompréhensible et que le nombre, à travers l’intelligence, parle, en symbole, pour découvrir la réalité ontologique. C’est donc la dimension symbolique, analogique, nous dirions métaphorique des nombres, qui nous interpelle. Pythagore aurait été, ainsi, à l’origine, entre autres, de :
La symbolique des pairs et impairs
– l’impair, limité, Un, droite, mâle, en repos, rectiligne, lumière, bien, carré, domine, équilibrant, avec une partie médiane, l’unité, deux parties symétriques. Dans le monde, l’impair sera donc le principe de la totalité puisqu’il comporte un commencement, un milieu et une fin.
– Le pair apparaît, par opposition dans le principe de la dualité de l’existant, illimité, multiple, gauche, femelle, en mouvement, courbe, obscurité, mauvais, oblong.
On peut dire que notre premier grade s’appuie aussi sur ce symbolisme de la dualité pythagoricienne.
La fameuse Tétraktys
Bien sûr sa forme triangulaire montre à l’évidence le 3, la réconciliation de la dualité dans son principe qui est l’unité, l’harmonie universelle. La triade est le nombre du tout, comme le reconnaît Aristote, «c’est le nombre 3 qui définit tout et toutes choses puisque ce sont les constituants du commencement, milieu et fin». C’est pour cela que 3 fut choisi comme base numéraire. Est-ce Zoroastre qui inspira Pythagore dont la doctrine était exposée dans ses Oracles, «le ternaire partout brille dans l’Univers et la Monade est son principe» et, selon Servius, les pythagoriciens assignèrent au Dieu suprême le trois qui est parfait, car il a un commencement, un milieu et une fin. Les pythagoriciens choisirent, naturellement, le triangle pour représenter le nombre 3.
Voici bien un des premiers symboles maçonniques.
Cette forme, mise en exergue dans le temple par sa position géographique, comme point focal, dans l’est des commencements de la lumière, delta lumineux, daleth hébraïque est donc la porte d’un ailleurs. Elle est une épure de toutes les tétrades pythagoriciennes, un plérome, une forme imaginale de la progression dynamique des illimités et des limitants. Selon Philolaos, qui à l’époque de Socrate transcrivait la mémoire du maître, «les illimités et les limitant, en s’harmonisant, constituent, au sein du monde, la nature, ainsi que la totalité du monde et ce qu’il contient». En somme, la triangulation, c’est l’enveloppe qui montre les mystères de la nature.
Les pythagoriciens distinguaient, en fait, 11 tétrades exprimant la pensée analogique et gnostique que Pythagore synthétisa, sans doute, à partir de ce qu’il avait appris ou conçu et qu’il enseigna. Chaque tétrade est, non une collection, un inventaire, mais une progression arithmétique, harmonique, géométrique, physique ou biologique qui conduit du point au volume, de l’homme à la cité, de la naissance au déclin. Chaque élément engendre et limite le suivant comme le point est l’origine et la limite de la ligne, la ligne celle de la surface, la surface celle du solide. La tétrade est un métalangage, une forme pour dire comment le monde de la réalité est issu de l’unité primordiale à travers les principes exprimés par les nombres. Aristote reconnaissait aux pythagoriciens le mérite d’avoir été les premiers à poser la question de l’essence et à avoir tenté de la définir.
1 – La première tétrade est le triangle enchâssant le nombre parfait 10, représenté par 10 points répartis en triangle sur 4 lignes. Il s’agit de la tétrade originelle qui est l’addition des 4 premiers nombres et conduisant progressivement au principe du nombre 10, en même temps qu’elle engendre les 4 consonances de la gamme (première, quarte, quinte, octave). Selon la tradition, Pythagore, par l’observation et l’expérience, avait découvert que les rapports entre la longueur des 4 cordes du tétracorde par rapport à la première étaient exprimés par les rapports numériques 4/3, 3/2, 2/1. La tétraktys donnait la clef des mystères de l’acoustique et les pythagoriciens étendirent à tous les domaines de la physique les conclusions de cette découverte. La formule du serment pythagoricien, transmises par différents auteurs et que l’on trouve dans les vers dorés sacralise la tétraktys : «Je le jure par celui qui a transmis à notre âme la tétraktys en qui se trouvent la source et la racine de l’éternelle Nature».
Certains font l’hypothèse que Pythagore rapporta, de son séjour de près de 20 ans en Égypte, la compréhension du mystère des pyramides : la pyramide de Khéops, qui semble n’avoir jamais recelé aucune momie de pharaon, ne serait-elle pas une forme sanctifiée du divin ? Ses dimensions représentant la compréhension du divin se déployant, et cette incarnation de l’intelligence divine aurait été reformulée par la tétraktys ? Qu’est-ce que Dieu, demandait saint Bernard ; il est longueur, largeur, hauteur, profondeur. La pyramide serait le symbole de toute la création, une représentation mathématique du fonctionnement de l’Univers. Dans ses dimensions se trouveraient encodées les vérités fondamentales de notre monde. Dans ce conservatoire des nombres est exprimée l’actualisation de la possibilité, c’est-à-dire l’Être, l’assurance que tout est vivant, que le Présent est éternel, la simultanéité du Temps, la notion de Tri-unité du Seul et Unique. Cela est une Connaissance que les francs-maçons atteignent par l’expérience que procure un apprentissage graduel et hiérarchisé.
Un nombre n’est pas une valeur abstraite, c’est une «vertu intrinsèque et active de l’Un suprême, de Dieu, source de l’harmonie universelle» nous rappelle Édouard Schuré, dans Les grands initiés.
2 – 3 la deuxième et troisième tétrade embrassent, dans une double progression géométrique de raison 2 et 3, la nature de toutes les grandeurs : le point, la ligne droite, la ligne circulaire, la surface plane, la surface courbe, le solide à surfaces courbes, le solide à surfaces planes.
4 – La quatrième tétrade est physique avec 1 = le feu, 2 = l’air, 3 = l’eau, 4 = la terre qui sont nos purifications lors des voyages de l’initiation.
5 – La cinquième, celles des figures géométriques associant les 4 premiers polyèdres aux 4 éléments.
6 – La sixième, celle des choses engendrées à laquelle Aristote accorde la génération du vivant à partir de la semence et son augmentation dans les trois directions, largeur, longueur, hauteur.
7 – La septième concerne le développement de la société : homme, famille, bourg, cité.
8 – La huitième présente les facultés cognitives qui assurent la connaissance des tétrades précédentes : pensée, science, opinion, sensation.
9 – La neuvième distingue les quatre dimensions de l’être animé : âme raisonnable, âme irascible, âme concupiscible, corps.
10 – La dixième celle du temps avec ses 4 saisons : printemps, été, automne, hiver.
11 – La dernière celle des âges de la vie : enfance, adolescence, maturité, vieillesse.
Ainsi les tétrades dévoilent l’Unité génétique de toutes choses en train d’accomplir leur achèvement comme les séphiroth dans l’arbre de vie.
Le delta lumineux serait donc, aussi, une tétrade, un plérome, une représentation systématique nous répondant à la question d’où vient le monde et comment il se déploie.
L’importance de la Tétraktys pythagoricienne dans n’importe quel type de connaissance métaphysique et cosmogonique est évidente. Le rapport des harmonies musicales avec les nombres est également un thème pythagoricien que la Maçonnerie et le Corpus Hermeticum reprennent sous forme de degrés et touches de reconnaissance liés aux sphères planétaires et aux Régents qui les gouvernent.
Il faudrait y ajouter les différents théorèmes pythagoriciens, sachant l’importance que l’art et la science de construire ont pour la Maçonnerie. Parmi eux, il suffirait de signaler celui du triangle rectangle, qui formé avec les nombres de la triade «3, 4, 5» est dit égyptien avec son hypoténuse (corde tendue entre les opposés) ressemblant si grandement à la corde des harpédonaptes marquée par des nœuds en 3, 4, 5. Et si chacun sait que la somme des carrés des côtés est égale au carré de l’hypoténuse, il est amusant de souligner les propriétés suivantes : dans un triangle rectangle de nombres entiers premiers entre eux on a toujours : -un côté pair et deux côtés impairs -l’hypoténuse est toujours la somme d’un carré pair et d’un carré impair -l’hypoténuse n’est jamais un multiple de 3 -le côté pair est toujours un multiple de 4 -Un des côtés est toujours un multiple de 5 -le périmètre est pair et la surface multiple de 6
Le nombre d’or.
Cette proportion d’harmonie, dite aussi dorée, est dérivée du rapport d’analogie a/b = c/d quand on réduit les quatre termes à deux en conservant le même rapport, soit a/b = a+b/a. Nous devrions dire les nombres d’or, que Pythagore et sa femme bien-aimée Théano déclinèrent dans tous les sens possibles, sous toutes leurs formes possibles de rectangle, de pentacle, d’étoile ou de pentagone, les traquant et mettant ainsi en valeur les théorèmes de Thalès. Dans cette irrationalité mathématique, de Pi et de Phi, qui ne se mesure pas mais se montre dans les lois de la diagonale et du cercle, dans l’infini de leur décimales, ils virent sans doute cette part inachevée du monde en train de s’actualiser dans le temps et la forme ; cela paraît être la beauté divine des nombres eux-mêmes.
La physionomie des nombres
Les nombres ont une physionomie et, selon celle-ci, ils sont nommés parfaits (somme des diviseurs du nombre redonne le nombre (par exemple les 3 seuls nombres parfaits compris entre 1 et 1000 soit 6, 28, 486), amicaux (la somme de diviseurs de l’un donne l’autre, 220 et 284), impairs ou pairs, triangulaires (3, 6, 10, 15), carrés (1, 4, 9,16), cubiques (1, 8, 27), rationnels, irrationnels, incommensurables. Quel vertige, quelle source pour la guématrie des cabalistes et, par là même, pour nous francs-maçons.
L’alphabet secret
Selon Oswald Wirth, inspiré des pythagoriciens, tel que l’a formulé Théon de Smyrne (IIe siècle av. J.-C.), l’alphabet secret élaboré par Pythagore serait la source de notre table à tracer appelée aussi table tripartite avec 2 parallèles verticales et 2 parallèles horizontales délimitant 9 cases dont les limites symbolisent les lettres qui leur sont affectées[4]. Elle indique aux francs-maçons que leurs constructions doivent se baser sur les propriétés des nombres ou de la géométrie et, symboliquement, que les travaux maçonniques doivent être exécutés en tenant compte des propriétés des nombres sacrés.
Ne sera pas évoqué ici ce en quoi le regard et l’écoute du ciel par Pythagore, à travers l’harmonique des rapports mathématiques, nous permet d’entendre les planètes bruire les notes de la gamme en tournant sur elles-mêmes autour du soleil.
L’art géométrique de la Franc-maçonnerie découle de la géométrie et de l’arithmétique pythagoriciennes parce que d’après les attestations de Proclus «à part quelques propriétés géométriques attribuées, sans doute à tort, à Thalès, les pythagoriciens ont été les premiers à étudier la géométrie et les nombres». La compréhension des nombres pythagoriciens facilite la compréhension des nombres sacrés maçonniques.
En conclusion sur cette première partie : même si Pythagore n’a rien «inventé», il a reconnu, dans la série décimale qui retourne à son Origine (10 = 1 + 0 = 1), une échelle naturelle, une lumière sur les mystères qui permettrait à l’être humain de compléter l’œuvre et d’opérer ainsi la transmutation en Homme Véritable, paradigme de tout initié, situé entre l’équerre et le compas.
2 – L’enseignement éthique
Mais, c’est sur cette autre part de son enseignement, l’éthique, que Pythagore va aussi inspirer les sources maçonniques.
Selon Céline Renooz, dans son livre Ère de vérité, histoire de la pensée humaine et de l’évolution morale de l’humanité à travers les âges et chez tous les peuples, «au milieu des luttes religieuses, le VIe siècle vit se produire une réaction contre le nouvel Hellénisme, c’est-à-dire contre le désordre moral des nouveaux cultes ; il y eut un retour momentané aux grandes idées du passé. Une école se fonda dans laquelle on enseignait les lois de la Nature telles qu’elles avaient été formulées dans la brillante époque de la primitive religion pélasgique [les ancêtres étrusques]. C’est l’école pythagoricienne, dans laquelle on donnait l’enseignement de la science aux prêtresses grecques, les Pythies» (p.437).
Selon la légende, c’est à Crotone, en Italie du Sud (qui faisait à l’époque partie de la Grèce), que Pythagore, trouvant refuge, reçut le soutien de l’homme le plus riche de la ville, Milon, dont il épousa la fille Théano (à laquelle Renooz attribue la réalité de la création de l’école en tant que prêtresse de la Pythie[5]). Toujours est-il que, dans cette volonté de masculinisation, l’Histoire retiendra que c’est Pythagore, avec sa femme toutefois, qui fonda l’école mixte pythagoricienne, connue aussi sous le nom de Fraternité pythagoricienne. Les femmes purent partager l’enseignement, elles furent environ 15% des initiés. Cela est un des signes de la très grande tolérance exigée dans le comportement des initiés de l’école pythagoricienne.
On y enseignait de nombreuses disciplines, comme les mathématiques ou la philosophie. On pourrait dire que c’était une sorte d’institut, un genre de monastère qui n’est pas sans rappeler la Castalie du Jeu des perles de verre d’Hermann Hesse, une association scientifique, philosophique, politique et religieuse avec règles de vie et d’éthique.
L’École pythagoricienne était une véritable école initiatique et le savoir mathématique soumis au secret. Le recrutement des membres de l’ordre était fait avec un soin scrupuleux. Pythagore, dit-on, étudiait sévèrement la vocation des jeunes gens qui se présentaient à lui, avant de les admettre aux premières initiations de cette vie nouvelle ; il cherchait à lire sur leur visage, à deviner dans leur démarche, dans leurs attitudes, dans toutes les habitudes de leur personne, les penchants de leur âme, le fond vrai de leur caractère, les aptitudes propres de leur esprit. Voici le principe des enquêtes maçonniques, n’est-ce pas ?
Les membres de l’École étaient séparés en deux groupes. Un rideau était tiré au milieu de la salle où Pythagore professait. Les élèves devaient écouter. Ils n’avaient pas le droit de parler durant les cours. Le silence de l’apprenti est comme celui de l’élève. Les exotériques se tenaient de l’autre côté du rideau et pouvaient seulement l’entendre. Les ésotériques se trouvaient du même côté que Pythagore. Cela avait une extrême importance dans la vie de l’École. Pythagore voulait savoir si les membres étaient capables de se taire et de garder secret ce qu’ils avaient entendu. Après cinq ans, un exotérique était autorisé à traverser le rideau. Cela marquait une étape importante dans la vie de l’École. Appellerions-nous cela une augmentation de salaire ?
Les textes des pythagoriciens étaient eux aussi soumis au secret. Rédigés dans un langage à double sens, ils jouaient sur deux niveaux d’interprétation ; l’un compris par tout le monde, l’autre réservé aux seuls initiés. Les pythagoriciens parlaient de sumbola et d’ainigmata.
Pour eux aussi, tout était symbole.
La plupart des connaissances se transmettaient de bouche à oreille. Cela donna lieu à une seconde séparation. Il y avait les acousmatiques (les auditeurs) à qui l’on transmettait les résultats mais pas les démonstrations pour y parvenir, et les mathématiciens (les apprenants) qui avaient le droit à ces dernières. Tout cela n’est pas sans rappeler notre organisation où, à chaque degré, des mystères sont dévoilés avec progression, ce qui fait de la Franc-maçonnerie une société initiatique et progressive.
Tous les membres de l’École devaient exercer leur mémoire. Chaque matin, ils devaient se remémorer ce qu’ils avaient fait, ce qu’ils avaient vu, ce qu’ils avaient entendu, ce qu’ils avaient dit la veille. En se présentant à l’École, chaque prétendant devait remettre tous ses biens à la communauté. Le dépouillement des métaux ne serait-il pas une reprise symbolique de cette règle ? Celui qui était renvoyé, cependant, recevait à son départ le double des biens qu’il avait déposés. On lui donnait en argent ce qu’il n’avait pas su prendre en savoir. L’expression «recevoir son salaire» correspond aussi en Franc-maçonnerie à une valeur-savoir. Mais, dès que son exclusion était prononcée, on lui creusait un tombeau. Il s’agissait d’une mort symbolique.
Pythagore disait sa théorie et laissait ses élèves le contredire. Cela lui permettait de savoir si ses élèves étaient capables de réfléchir par eux-mêmes et les conviait à quitter l’école s’ils n’étaient pas satisfaisants, refusant un savoir de perroquet. La Maçonnerie n’est pas une science mais un art, celui d’éveiller les consciences, cet effort est au départ individuel. C’était surtout, offrir une grande liberté individuelle de penser et même de conscience. «Il faut avoir une religion, garde ta foi jurée». Il y a ici, dans ce vers doré, une relation entre l’universel et le particulier, une exigence de tolérance. Toutes nos constitutions évoquent, comme un impératif primordial la liberté de conscience de chacun. Les vers dorés sont une des premières tentatives de corpus moral théorique et pratique, philosophique, spirituel et œcuménique.
Vouloir rendre compte de Pythagore revient en fait à essayer de reprendre les fouilles des traces textuelles laissées par ses disciples ou par les historiens de cette époque, à narrer chacun des instants de sa vie exemplaire parce que sa parole était fraternelle et son vécu conforme à son enseignement. Les biographies de Pythagore, rédigées par Porphyre et Jamblique, fixèrent définitivement les traits caractéristiques du sage idéal, modèle de vertu, de piété et de sagesse, que tout adepte d’un platonisme mâtiné de pythagorisme devait imiter pour se revendiquer de cette famille spirituelle qui inspira, probablement, les premiers textes maçonniques. La Maçonnerie est aussi la médiation entre la théorie et la pratique par le biais de l’instruction, non d’un savoir désincarné, mais de l’exemple. Le franc-maçon pratique l’éthique qui est bien ce qui se produit librement, sans contrainte externe, par un sentiment d’obligation morale interne.
Ce qui est incontestable, c’est que Pythagore s’était proposé un but moral et religieux. Il avait voulu, dit l’historien Zeller, fonder une école de piété, de bonnes mœurs, de tempérance, de courage, d’ordre, d’obéissance à la loi, de fidélité dans l’amitié. Il y a trop de similitudes avec l’esprit des premiers textes maçonniques pour que ce ne soit qu’un hasard, l’influence semble indéniable. Le lien entre la Franc-maçonnerie et l’Ordre pythagoricien, sans qu’il s’agisse d’une dérivation historique ininterrompue, seulement d’une filiation spirituelle, est certain et manifeste.
Pour plagier Saint Thomas qui disait que «le mot est comme un miroir dans lequel on voit la chose», ne pourrions-nous dire que le franc-maçon est comme un miroir dans lequel on voit Pythagore ?
[1] Pour garder un esprit critique sur l’attribution à Thalès de son fameux théorème, se reporter à l’article d’Alain Herreman , Aux sources du « théorème de Thalès », Sur la condescendance et la recherche de l’origine.
[2] À lire l’article de Michel Serres, Gnomon: les débuts de la géométrie en Grèce, condensé du chapitre De la pyramide au tétraèdre, dans son éblouissant ouvrage Les origines de la géométrie (p.195 à 270).
[3] Sur ce sujet, consulter l’article de Paul-Henri Michel, Les médiétés.
[4] Pour Arturo Reghini, dans son opus Les nombres sacrés dans la Tradition Pythagoricienne maçonnique, il semble hors de doute que l’origine de la table à tracer remonte à la table de Théon.
[5] Théano était une Prêtresse qui avait gardé le dépôt sacré de la tradition scientifique et qui voulut en faire un enseignement régulier. Les historiens masculins diront, dans leur langage symbolique, qu’elle livra le Palladium aux Grecs, c’est-à-dire qu’elle enseigna la science cachée, quoique son École constituât une société fermée comme les ordres secrets, un Collège d’initiés, une sorte de congrégation sacrée (p.439 de l’ouvrage cité).
Le fameux triangle de Pythagore
Ce théorème stipule que, sous son aspect mathématique et dans un univers euclidien, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Le théorème de Pythagore a eu différents noms : théorème de la mariée chez les Grecs, chaise de la mariée chez les Hindous, figure de l’épousée chez les Perses pour la réciproque, maître de la mathématique au Moyen âge, pont aux ânes pour les collégiens du XIXe siècle.
Giamblicus, le biographe de Pythagore, nous conte l’anecdote suivante : quand le Maître s’est rendu compte du sens caché du théorème , il fut tellement frappé par la profondeur du mystère entrevu qu’il crut avoir eu une révélation divine. La légende, qui dit que Pythagore aurait sacrifié 100 bœufs lorsqu’il eut trouvé le théorème de l’hypoténuse, est un non-sens car les seules offrandes acceptées dans le pythagorisme étaient des offrandes végétales préparées.

Pythagore n’en a pas fait de démonstration, aussi, à son époque on devait parler de la règle de Pythagore et non de théorème. En effet, les démonstrations les plus anciennes qui nous soient parvenues lui sont postérieures, celles d’Euclide en particulier[2] avec le théorème 33 dans la 47ème proposition du Livre I et le théorème 21 de sa 31ème proposition du Livre VI qui généralise les rapports des surfaces des figures. Ces propositions ont un aspect géométrique exprimant une égalité de surfaces et non de calcul : «Dans les triangles rectangles, la figure construite sur le côté qui sous-tend l’angle droit, est égale aux figures semblables et semblablement décrites sur les côtés qui comprennent l’angle droit.» Euclide affirme donc la primauté de la matérialité sur l’abstraction numérique. Cependant le résultat semblait déjà connu, en Mésopotamie, plus de mille ans avant Pythagore[1].
Les valeurs des carrés ne sont pas un ensemble de nombres, mais une nouvelle entité élevée sur elle-même, qui contient en synthèse les propriétés et les qualités des nombres qui l’ont produite. Le carré du nombre de l’homme caractérise le passage d’un état naturel à un état spirituel, soit l’exhaussement de l’esprit en l’homme, à l’exemple du sommet de la pierre cubique à pointe.
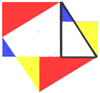
Le théorème chinois de Guogu[3], reconstitué d’après les commentaires du mathématicien chinois Liu Hui utilise le principe du puzzle : deux surfaces égales après découpage et recomposition ont même aire.

Dans un article analysant la signification ésotérique du triangle de Pythagore, Antonietta Francini cite Plutarque, qui décrit et explique la signification égyptienne antique de ce triangle, où le côté droit est assimilé au mâle (Osiris), la base à la femelle (Isis), et l’hypoténuse au résultat de leur union (Horus). Plutarque écrit: «Trois est le premier nombre impair parfait; quatre est un carré dont le côté est le nombre pair deux; mais cinq est en quelque sorte semblable à son père, et en quelque sorte semblable à sa mère, étant composé de trois et deux.

Ce théorème de Pythagore est inscrit, sous forme géométrique, entre les deux personnages principaux du frontispice de la première édition des Constitutions d’Anderson de 1723. On peut lire le mot écrit en grec ευρηχα (Eurèka) sous la figure. Selon Vitruve, c’est Archimède qui aurait prononcé cette expression, en attestant, par ses expériences, la composition en or de la couronne du roi Hiéron par la mesure de la masse volumique d’eau déplacé par celle-ci. C’est une expression jubilatoire d’avoir découvert une solution scientifique aux mystères du monde.

On en retrouve sa symbolique dans l’équerre du bijou porté par le passé Vénérable maître, faisant souvent apparaître la démonstration d’Euclide, témoignant pour la géométrie de son importance centrale dans la pensée maçonnique.
Le triangle de Képler associe le théorème de Pythagore et le nombre d’or par la figure construite à partir du rectangle d’or (parfois appelé le visage de Dieu), où les dimensions respectives des côtés du triangle sont : Φ, racine de Φ et 1.
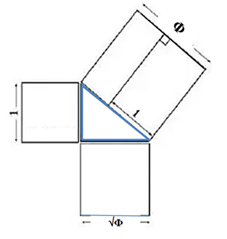
Pour marier les côtés : Dans un triangle rectangle de nombres entiers premiers entre eux, on a toujours un côté pair et deux côtés impairs, l’hypoténuse est toujours la somme d’un carré de pair et d’un carré d’impair, le périmètre est pair, la surface est paire car multiple de 6.
Vous retrouverez d’autres usages du théorème dans mon ouvrage «Tracés maçonniques», éditions Numérilivre, prévu pour septembre 2022
[1] On établit que Pythagore serait né vers la fin du VIe av J.-C.
[2] IVe siècle av. J.-C.
[3] IIIe siècle