Réfléchissons un peu à ce qu’est une démonstration : c’est une suite d’arguments implacables qui filent d’une hypothèse supposée vraie jusqu’à une conclusion, comme un train express sans arrêts imprévus.
Si vous voulez démontrer le théorème de Pythagore, par exemple, il faut bien partir de quelque chose, disons le théorème de Thalès, parce que… Pourquoi pas ? Et pour démontrer Thalès, vous devrez repartir d’autre chose, et ainsi de suite, comme un jeu de dominos infini qui refuse de tomber.
À un moment donné, il faut bien s’arrêter et planter un drapeau sur une vérité qu’on affirme vraie sans la démontrer, parce que sinon, on y passerait l’éternité. C’est obligé ! On appelle ça un axiome, ce petit malin qui se la joue «je suis vrai, point final». Un peu comme l’ouverture des travaux rituels maçonniques qui font passer du profane au sacré !
Alors, vous me direz : «En quoi les axiomes sont-ils vrais, hein ?» Eh bien, il y a plusieurs espèces de mathématiciens, comme des races de chats capricieux. Il y en a qui s’en fichent royalement : «Peu importe si c’est vrai, du moment que c’est cohérent !» Eux, ce qui les branche, c’est la chaîne logique, la démonstration qui claque comme un fouet.
Par exemple, voici une démonstration célèbre que 1 + 1 = 2, planquée en bas de la page 379 d’un bouquin de Russell et Whitehead – oui, il leur a fallu 378 pages pour en arriver là, ces farceurs
Mais d’autres mathématiciens, plus terre-à-terre, disent qu’un axiome est vrai s’il colle à ce qu’on voit ou ressent dans le monde réel, genre «ça rend compte de la réalité, comme un miroir sans buée».
Du coup, à travers les axiomes, les maths flirtent avec le monde physique, un peu comme un rendez-vous galant avec la physique.
Prenez la géométrie qu’on nous bassine à l’école : cercles, triangles, et tout le tintouin. Il y a plus de 2300 ans, Euclide a compilé un livre génial, Les Éléments , où il a entassé toutes les maths de son époque. Bien sûr, il avait besoin d’axiomes. La plupart sont incontestables, style «deux quantités égales à une troisième sont égales entre elles» – waouh, Sherlock, merci pour l’info !
Mais il y en a un qui a semé la zizanie : le cinquième. Imaginez : une droite bleue dans un plan, un point rouge à côté. L’axiome dit qu’il existe une seule droite parallèle à la droite bleue passant par ce point rouge. Évident, non ? Pas besoin de démontrer, c’est un axiome, point barre !
Pendant des siècles, personne n’a moufté. C’était clair comme de l’eau de roche. En 1196, Maïmonide va même jusqu’à dire que Dieu, malgré sa toute-puissance et sa liberté infinie, ne pourrait pas créer quelque chose qui contredise la logique d’Aristote ou la géométrie d’Euclide. Vous voyez ? Les mathématiciens plus balèzes que Dieu lui-même ! Kant, plus tard, enseigne que cette géométrie est câblée dans notre cerveau, innée, comme un logiciel préinstallé – pas de mise à jour nécessaire.
Mais creusons un peu ces parallèles. Mettez-vous à la place des Grecs anciens : ils voyaient le monde comme une boule finie, limitée par une sphère des étoiles fixes, genre un globe de Noël cosmique. Deux parallèles qui osent se couper au-delà ? Impossible, vu que le point de croisement n’existe même pas ! Le concept de parallèles présuppose un espace infini, ce que les Grecs refusaient poliment – «Non merci, on est bien dans notre petit monde clos».
Il a fallu attendre le début du 19e siècle pour que trois mathématiciens rebelles – Gauss, Bolyai et Lobatchevski, des esprits libres genre rockstars des maths – osent tout chambouler. Indépendamment, à peu près en même temps, ils pondent un axiome alternatif : par un point extérieur à une droite, il existe une infinité de parallèles ! Et boum, ils bâtissent une géométrie aussi jolie que celle d’Euclide, cohérente, pleine de théorèmes… mais où Pythagore se prend une claque, car son théorème ne tient plus la route. Bolyai écrit à son papa : «À partir du néant, j’ai créé un nouveau monde !» Plus fort que Dieu, je vous dis – et sans budget effets spéciaux !
Évidemment, les contemporains ont fait la grimace : «Un nouveau monde ? Pff, on n’en veut pas !» Gauss, lui, garde sa découverte secrète, persuadé que c’est trop dangereux – imaginez, casser la philosophie de Kant ? C’est comme dire à un chef que sa recette est périmée !
Il faut attendre la fin du 19e, début 20e siècle, pour que ça devienne «raisonnable». Et qui rend ça digeste ? Poincaré, en 1902, avec un texte de vulgarisation hilarant. Il dit : «Imaginez un monde enfermé dans un grand cercle, avec une température qui chute du centre vers les bords, jusqu’au zéro absolu aux limites. Les objets rapetissent en s’approchant du bord.» Pour les habitants, ce monde semble infini : plus ils avancent vers le bord, plus ils rétrécissent, leurs pas deviennent minuscules, impossible d’atteindre la limite ! Ils ne s’en rendent pas compte – leur mètre ruban rapetisse aussi. Mais pour nous, observateurs extérieurs, c’est clair comme du cristal.
Dans ce monde, le plus court chemin est un arc de cercle perpendiculaire au bord – leurs «droites» sont nos cercles ! Et l’axiome d’Euclide ? Kaput ! Une infinité de parallèles par un point. Ces gens sont raisonnables, ils vivent normalement, ignorant qu’ils rapetissent – comme nous, qui ignorons probablement des tas de trucs absurdes.
La morale de Poincaré ? On peut inventer plein de mondes géométriques raisonnables, chacun avec sa logique, et en piocher un pour éclairer notre réalité. Comme un artisan qui choisit son outil : «Une géométrie n’est pas plus vraie qu’une autre, elle est juste plus commode.» Moi, j’y vois un message de liberté : adieu le carcan d’Euclide, bonjour la création de mondes ! Eddington l’a dit :
«La libération de l’espace-temps est un rêve de poète et mystique, mais ce sont les mathématiciens qui l’ont fait !»
Aujourd’hui, les maths jonglent avec des géométries sans sourciller – il y a 100 ans, c’était impensable. Ce vent de liberté a débordé : Einstein mélange espace et temps dans une géométrie non-euclidienne pour sa relativité. Les artistes s’en emparent : fini les perspectives forcées des Beaux-Arts ! Regardez ce tableau de Max Ernst en 1942 : «Jeune homme intrigué par une mouche non-euclidienne» – oui, même les mouches se rebellent !
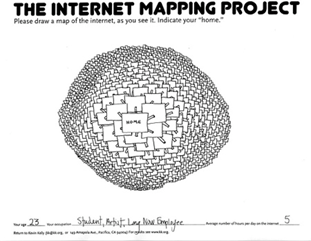
Et Internet ? Un projet génial, l’Internet Mapping Project. demande aux gens de dessiner leur vision d’Internet. Des centaines de croquis fous, et beaucoup ressemblent au disque de Poincaré : tout rapetisse vers les bords ! Un internaute a crayonné Internet comme un monde où les sites s’entassent au centre et s’éloignent en miniaturisant – non-euclidien pur jus !
Une élucubration pour finir : quand j’étais gamin, mon monde était un cercle de 5 km autour de la maison, et Euclide suffisait amplement pour mes bêtises enfantines. Mais nos gosses d’aujourd’hui naviguent dans des géométries multiples : Internet, Facebook, et même le réseau SNCF, où Paris est plus «proche» de Lyon que de certaines banlieues ! Pourquoi ne pas leur enseigner un peu de géométrie des réseaux à l’école ? Ça forcerait à zapper un peu d’Euclide et son Pythagore poussiéreux – et franchement, ça ne me dérangerait pas du tout.
Pour clore, profitez des conférences Ernest : je parie que Gauss, Bolyai et Lobatchevski ont, à leur façon tordue, un peu chamboulé votre vision du monde. Et si vous n’êtes pas d’accord, eh bien, prouvez-le avec un axiome humoristique !
Inspiré par Étienne Ghys, Et si le théorème de Pythagore n’était pas vrai ? «Les Ernest»
Bravo Solange pour cet article plein d’allant primesautier et souriant. Aimons les mathématiciens et les physiciens comme nous aimons nos mystères. Les barrières qui séparent encore les scientifiques rationnels des ésotéristes intuitifs tombent comme des châteaux de cartes, au grand dam des académies poussiéreuses et des religions dogmatiques qui gouvernent encore le monde.
De grands scientifiques mènent aussi ce combat, au risque de voir supprimer leurs crédits de recherche.